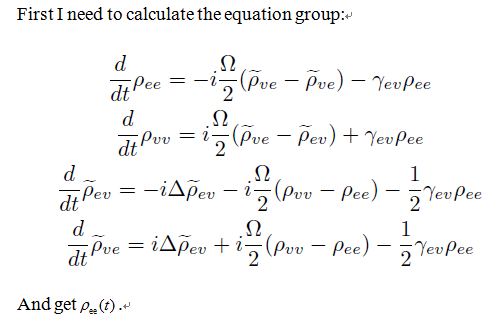
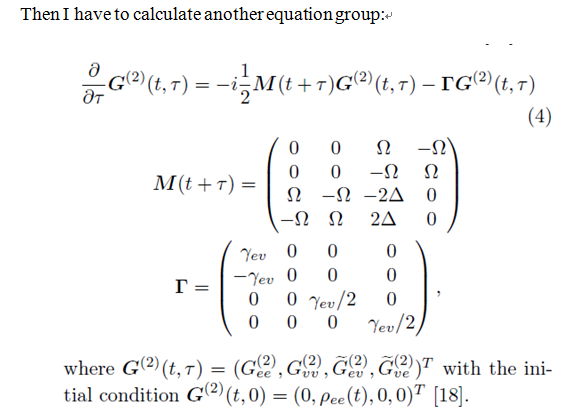
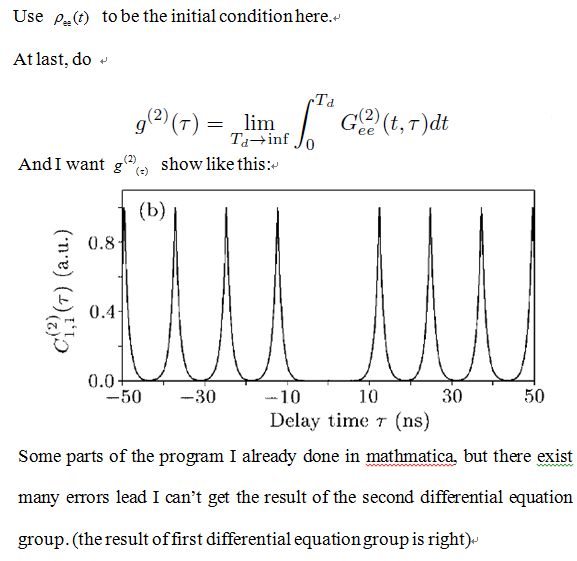
and when I calculate the second equation group, the error appear? How can I solve this problem?
(*Population equations*)
Clear["Global`*"];
\[Epsilon] = 10; (* \[Epsilon] *)
\[Gamma]10 = 1; (* \[Gamma]10 *)
a = 0.108; (* a *)
pump[t_, \[Epsilon]_, a_] := \[Epsilon]*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 0\), \(100\)]
\*SuperscriptBox[\(E\), \(-\((Abs[t - 12.5 i]/a)\)^2\)]\);
\[CapitalDelta] = 0; NDSolve[{r11'[
t] == -(1/2) I*
pump[t, \[Epsilon], a]*(r01[t] - r10[t]) - \[Gamma]10*r11[t],
r00'[t] ==
1/2 I*pump[t, \[Epsilon], a]*(r01[t] - r10[t]) + \[Gamma]10*r11[t],
r10'[t] == -I*\[CapitalDelta]*r10[t] -
1/2 I*pump[t, \[Epsilon], a]*r00[t] +
1/2 I*pump[t, \[Epsilon], a]*r11[t] - 1/2 \[Gamma]10*r10[t],
r01'[t] ==
I*\[CapitalDelta]*r10[t] + 1/2 I*pump[t, \[Epsilon], a]*r00[t] -
1/2 I*pump[t, \[Epsilon], a]*r11[t] - 1/2 \[Gamma]10*r10[t],
r00 [0] == 1, r11 [0] == 0, r10 [0] == 0, r01 [0] == 0}, {r11, r00,
r10, r01}, {t, 0, 500}];
r11 = r11 /. %[[1]];
\[Rho]11[t_] := Re[(r11[t])];
Plot[\[Rho]11[t], {t, 0, 45}, PlotRange -> {0, 1}]
(*Second-correlation equations*)
NDSolveValue[{\!\(
\*SubscriptBox[\(\[PartialD]\), \(\[Tau]\)]\(x11[t, \[Tau]]\)\) ==
1/2 I*pump[
t + \[Tau], \[Alpha], \[Eta]]*(x01[t, \[Tau]] -
x10[t, \[Tau]]) - \[Gamma]10*x11[t, \[Tau]], \!\(
\*SubscriptBox[\(\[PartialD]\), \(\[Tau]\)]\(x00[
t, \[Tau]]\)\) == -(1/2) I*
pump[t + \[Tau], \[Alpha], \[Eta]]*(x01[t, \[Tau]] -
x10[t, \[Tau]]) + \[Gamma]10*x11[t, \[Tau]], \!\(
\*SubscriptBox[\(\[PartialD]\), \(\[Tau]\)]\(x10[t, \[Tau]]\)\) ==
I*\[CapitalDelta]*x10[t, \[Tau]] +
1/2 I*pump[t + \[Tau], \[Alpha], \[Eta]]*x00[t, \[Tau]] -
1/2 I*pump[t + \[Tau], \[Alpha], \[Eta]]*x11[t, \[Tau]] -
1/2 \[Gamma]10*x10[t, \[Tau]],
\!\(
\*SubscriptBox[\(\[PartialD]\), \(\[Tau]\)]\(x01[
t, \[Tau]]\)\) == -I*\[CapitalDelta]*x10[t, \[Tau]] -
1/2 I*pump[t + \[Tau], \[Alpha], \[Eta]]*x00[t, \[Tau]] +
1/2 I*pump[t + \[Tau], \[Alpha], \[Eta]]*x11[t, \[Tau]] -
1/2 \[Gamma]10*x10[t, \[Tau]], x00 [t, 0] == \[Rho]11[t],
x11 [t, 0] == 0, x10 [t, 0] == 0, x01 [t, 0] == 0}, {x11, x00, x10,
x01}, {t, 0, 500}, {\[Tau], -30, 30}]
G[\[Tau]_] := NIntegrate[x00[t, \[Tau]], {t, 0, 450}]
Plot[G[\[Tau]], {\[Tau], -20, 20}, PlotRange -> All]
 Attachments:
Attachments: