Consider the following triangulated planar object
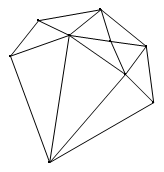
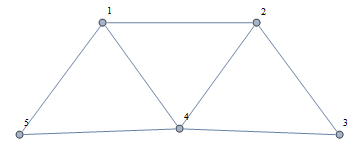
We notice that it has 10 triangular faces.In general, given a planar graph, how can we obtain these triangles? Take a simple graph, for instance
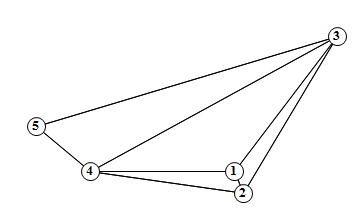
g1 = Graph[{1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 5,
1 \[UndirectedEdge] 4, 2 \[UndirectedEdge] 4,
2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 4,
4 \[UndirectedEdge] 5}, VertexLabels -> "Name", ImagePadding -> 10]
according to the theory, if m is its adjacency matrix (the adjacency matrix of a graph is a 0 - 1 matrix in which the i -j element is 1 only if vertices i and j are adjacent )
the number of its triangles is equal to the trace of m^3 divided by 6 (the trace of a matrix is the sum of its diagonal elements).
For this example
m1 = AdjacencyMatrix[g1];
m1 // MatrixForm
m1.m1.m1 // MatrixForm
Tr[m1.m1.m1]/6
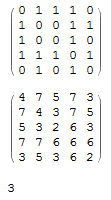
(if you are confused by the fact that the element at row 1 column 3 is 1, even though vertices 1 and 3 are not connected, check VertexList[g1])
Another example:
g2 = Graph[{1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 5,
1 \[UndirectedEdge] 6, 1 \[UndirectedEdge] 7,
1 \[UndirectedEdge] 10, 2 \[UndirectedEdge] 6,
2 \[UndirectedEdge] 7, 3 \[UndirectedEdge] 5,
3 \[UndirectedEdge] 8, 3 \[UndirectedEdge] 9,
3 \[UndirectedEdge] 10, 4 \[UndirectedEdge] 6,
4 \[UndirectedEdge] 8, 4 \[UndirectedEdge] 9,
5 \[UndirectedEdge] 6, 5 \[UndirectedEdge] 8,
5 \[UndirectedEdge] 10, 6 \[UndirectedEdge] 8,
7 \[UndirectedEdge] 10, 8 \[UndirectedEdge] 9},
VertexLabels -> "Name", ImagePadding -> 10]
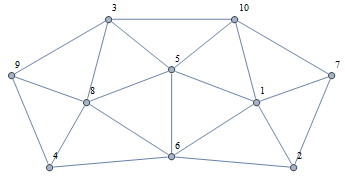
m2 = AdjacencyMatrix[g2];
MatrixForm[m2]
MatrixForm[m2.m2.m2]
Tr[m2.m2.m2]/6

Getting the indices of the vertices forming the triangles takes more work. An idea is as follows. Construct the matrix of "connections" :
t = Map[Flatten[Position[#, 1]] &, Normal[m2]]
{{2, 5, 6, 7, 10}, {1, 6, 7}, {5, 8, 9, 10}, {6, 8, 9}, {1, 3, 6, 8,
10}, {1, 2, 4, 5, 8}, {1, 2, 10}, {3, 4, 5, 6, 9}, {3, 4, 8}, {1, 3,
5, 7}}
and the "transformation of connections" :
tr = Thread[Range[10] -> t]
{1 -> {2, 5, 6, 7, 10}, 2 -> {1, 6, 7}, 3 -> {5, 8, 9, 10},
4 -> {6, 8, 9}, 5 -> {1, 3, 6, 8, 10}, 6 -> {1, 2, 4, 5, 8},
7 -> {1, 2, 10}, 8 -> {3, 4, 5, 6, 9}, 9 -> {3, 4, 8},
10 -> {1, 3, 5, 7}}
then apply it twice to t
t1 = (t /. tr);
t2 = (t1 /. tr);
and the following code gets the indices of the vertices of the triangles :
r = Map[Position[t2[[#]], #] &, Range[10]];
r2 = Table[ Map[{i, t[[i, First[#]]], t[[t[[i, First[#]]], #[[2]]]]} &, r[[i]]], {i, 10}];
tri = Union[Sort /@ Flatten[r2, 1]]
{{1, 2, 6}, {1, 2, 7}, {1, 5, 6}, {1, 5, 10}, {1, 7, 10}, {3, 5, 8}, {3, 5, 10}, {3, 8, 9}, {4, 6, 8}, {4, 8, 9}, {5, 6, 8}}
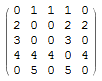
Alternatively, we might proceed as follows. Using our first example g1, let us substitute the adjacency matrix by the following one
(m3 = (Normal[m1] Range[5])) // MatrixForm
then we redefine the multiplication of matrices by taking addition as listing and multiplication as yuxtaposition. The square of the previous matrix would be
m4 = Table[
Select[Table[
10 m3[[i, k]] + m3[[k, j]], {k,
5}], (# > 9) \[And] (Mod[#, 10] > 0) &], {i, 5}, {j, 5}];
MatrixForm[m4]

and the cube of m3 would be
m5 = Table[
Select[Join @@
Table[10 m4[[i, k]] + m3[[k, j]], {k,
5}], (# > 9) \[And] (Mod[#, 10] > 0) &], {i, 5}, {j, 5}];
MatrixForm[m5]

Actually, only elements on the diagonal interests us so it is better if we do
m6 = Table[
Select[Join @@
Table[10 m4[[i, k]] + m3[[k, i]], {k,
5}], (# > 9) \[And] (Mod[#, 10] > 0) &], {i, 5}]
{{142, 143, 124, 134}, {241, 214, 254, 245}, {341, 314}, {421, 431,
412, 452, 413, 425}, {542, 524}}
then, the indices of the vertices of the triangles are
Select[Map[Mod[{Floor[#/100], Floor[#/10], #}, 10] &,
Flatten[m6]], OrderedQ]
{{1, 2, 4}, {1, 3, 4}, {2, 4, 5}}
Of course, the actual coordinates of the vertices of the graph have to be considered. For instance, we compute five triangles in the following graph.
pts = {{0.6, 0.5}, {0.7, 0.26}, {1.74, 2}, {-1, 0.5}, {-1.6, 1}};
segs = {1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 3,
1 \[UndirectedEdge] 4, 2 \[UndirectedEdge] 3,
2 \[UndirectedEdge] 4, 3 \[UndirectedEdge] 4,
3 \[UndirectedEdge] 5, 4 \[UndirectedEdge] 5};
m2 = AdjacencyMatrix[Graph[segs]];
Tr[m2.m2.m2]/6
5
but can you see them in its picture?
Graphics[{EdgeForm[Thin], ColorData[2, 6], Black,
Map[({a, v} = #; Line[Map[{pts[[a]], #} &, Part[pts, v]]]) &, t],
White, MapIndexed[{Disk[#1, .1],
Text[Style[#2[[1]], Black, 13, Bold], #1]} &, pts]},
PlotRange -> {{-2, 2}, {0, 2.5}}]
I suspect there must be other way of computing triangles by using Mathematica pattern matching capabilities. For instance, for g1 we have the list of its edges as
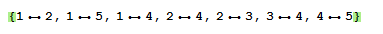
it must be possible to just say : search for all patterns of the form
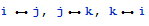
with i <> j <> k. How? How about all the faces in a graph? The pattern would be find all cycles of the form
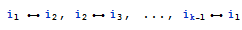
for all different i' s and k > 2. Of course, these faces have to be such that they dont contain other faces. How can we do it?