Terrence Tao recently published a proof of the Erdos discrepancy problem. There are also two papers by Boris Konev and Alexei Lisitsa, one giving the longest known sequence (1160) with discrepancy 2 (arXiv:1402.2184), and another giving the longest known sequence (130000) with discrepancy 3 (arXiv:1405.3097, data). The problem was being examined by the polymath project.
Consider a sequence like x_i = -1, 1, 1, -1, 1, -1, -1, 1, 1, -1, 1, 1, -1, and 1, where all the terms are +1 or -1. After that, partition x_i into sections of length d, take the first k sections, and then total up the last terms in each section. With d=3 and k=4, the sections would be (-1, 1, 1), (-1, 1, -1), (-1, 1, 1), (-1, 1, 1), the final terms would be 1, -1, 1, 1, and their total would be 2. The maximum value obtained by any considered k or d is the discrepancy.
Attached is an early look at a Demonstration I wrote to explore their results. Here's a simplified version. First a length 1160 dataset.
discrepancy1160 = Characters["-++-+--++-++-+--+--++-+--+--++-+--++-++-+-++--++-+---+-++-+--+--++++--+--++-+--++-++----++-++-+-++--++-+-+---++-+--++-++-+--++-+--+---+-++-+--++-++-+--+--++-++-+--++-+--+++-+-+----+++-+--+--+++---++-++-+--+--+++--+-+-+--+-+++-++-+--+--++-+--++-++-+--+--++--+++---+++-+---++-+--++--+-+--+-+++-+--++-++-+--++-+--+--++-+--++--+-++-+-+--+-+-++-+--++-+--+--++-+-+-++-+-+-++---+-+--++++--+---++-+-++-+--++-+--+--++-+--++++--+---+-++++--+--++-++-+--++-+--+--++-+--++-++-+--++-+--+--++-++-+----+++-+--++--+++---+-++-+--+-++---+-++-++-+--+--++--++++-+--+--+--++++--+--+++---++-++-+--++--+-+--+--++-++-+--+--+-+++-++-+--+--++--+-++-++-+--+--+--++-++-+--+++---++-+--++-++---+++---++-++----+++--+-++-+--+--++-+--++-++-+-++--++--++----+++-++--++----++-+++--++---+++----+-+-++-++-++-+-+----+++--++-+--++-++-+--+--+--++-+--++-++-+--++--+-+--+-+-+-++++---+-+-++--+--+-+-+-++-+-+++--+-+--+--+-+++--+-+++---++-+--+--++-++--++---++-+-++--++-+---+-++-+--+-++--++-+--++-+--+-+++-+--++--+-+-+++--+-+--++-++-+--+--+-++---+-++-+-++--++-+--+++-+----++--+-++-+-++--++-+--++-+-++--++-+---+-++-+--+++----+-+-++--++-+--++-++-++-+--+--+--++++---++---+-+-++-+-+++--+-++--+-+--+-+-++---+++-++"]/.{"+"-> 1, "-"-> -1};
Next, code for looking at it.
Manipulate[
Module[{data,k, adder,array},
{k=Floor[1160/d];
data = Table[discrepancy1160[[i d]],{i,1,k}];
adder =ReplacePart[Table[0 ,{1160}],Thread[Table[d i,{i,1,k}]->2]];
array = ArrayPlot[Partition[(discrepancy1160+1)/2 +adder,58], ImageSize-> {550,270}, Frame-> False,
PixelConstrained-> True,ColorRules->{0->White,1->LightGray,2-> Red,3-> Blue}]};
Column[{
ListPlot[FoldList[Plus,0,data], ImageSize-> {550,100}, AspectRatio-> 1/5, PlotRange-> All],array}, Alignment-> Center]],
Row[{Control[{{d,20,"multiplier"},1,100,1, Appearance-> "Labeled"}]}],
SaveDefinitions->True, ContentSize-> {570,400}]
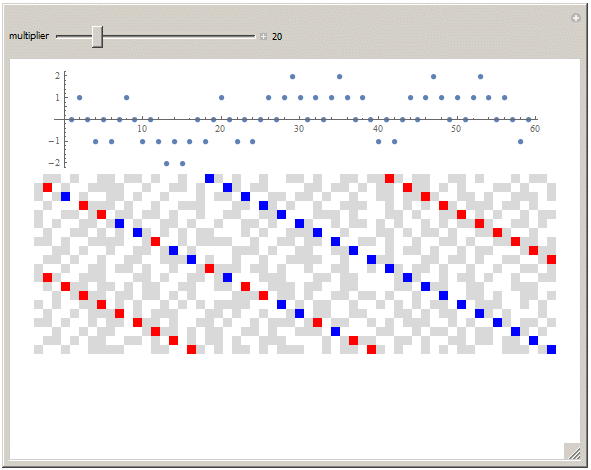
That's a look at a long sequence with discrepancy 2. In the proof by Terrence Tao, he mentions his first step was a Fourier-analytic reduction.
ListPlot[ReIm /@ Fourier[discrepancy1160], AspectRatio -> 1, Axes -> False, ImageSize -> {400, 400} ]
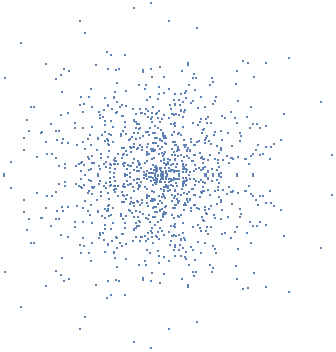
That doesn't seem to do much. Is there a neat Fourier-related picture to go with these extremal sequences? The attachment has the Demonstration version, which includes the dataset for discrepancy 3.
One suggestion I received:
Column[Table[ListPlot[{Abs, Im, Re}[[n]] /@ Fourier[discrepancy1160], Filling -> Axis, PlotRange -> All, ImageSize -> {540, 180},
AspectRatio -> 1/3], {n, 1, 3}]]
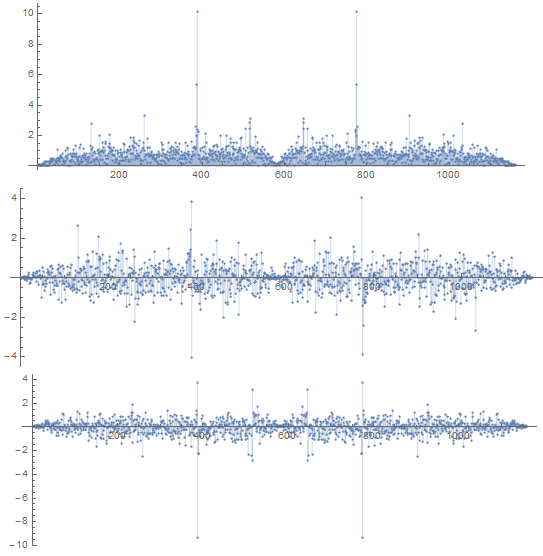
Perhaps a more meaningful transform for the scatterplot.
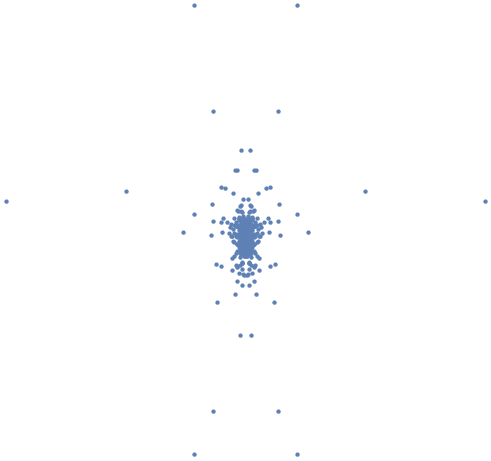
ListPlot[Reverse[ReIm[#]]&/@Fourier[discrepancy1160], PlotRange-> All, Axes-> False, AspectRatio-> 1,PlotStyle-> PointSize[Medium]]
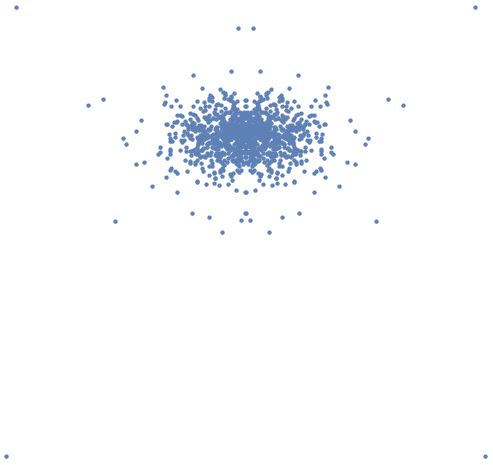
For those that want another Rorschach test, here's the result of that code on the discrepancy 3 dataset of length 130000 from the attachment.
 Attachments:
Attachments: