Message Boards Message Boards

GROUPS:
Wolfram Science Physics Dynamic Interactivity Wolfram Language
Vitaliy Kaurov

Quantum block cellular automaton NKS book page 1059

Vitaliy Kaurov, WOLFRAM Research
Posted 10 years ago
4370 Views
|
2 Replies
|
9 Total Likes
|
At Wolfram Science Summer School 2013 that is currently in progress, we came by an interesting system mentioned in the NKS book on the page 1059. It is a quantum block cellular automaton (CA) with unitary evolution that preserves magnitude of complex field. I thought it would be interesting to implement it. It is rather rare we come by a clear simple design for a quantum CA. Below initial conditions are to complex numbers IC1 and IC2 placed on background of zeros. The rule number runs continuous space from 0 to 2Pi and is the angle of unitary operator.
 Manipulate[ 
 data = NestList[step[a], ArrayPad[{IC1[[1]] + I IC1[[2]], 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, IC2[[1]] + I IC2[[2]]}, {15, 15}], 30]; 
 Grid[{{
 ArrayPlot[Abs[data], ColorFunction -> "DarkRainbow", Mesh -> True, Frame -> False, PlotRangePadding -> 0, ImageSize -> 300],    ArrayPlot[Arg[data], ColorFunction -> "DarkRainbow", Mesh -> True, Frame -> False, PlotRangePadding -> 0, ImageSize -> 300]
 }}, Spacings -> 0] , 
 {{a, 2.94, "rule"}, 0, 2 Pi, ImageSize -> Tiny} , 
 {IC1, {-1, -1}, {1, 1}} , 
 {IC2, {-1, -1}, {1, 1}} , 
 FrameMargins -> 0 , ControlPlacement -> Left , 
SaveDefinitions -> True , Initialization -> (
evo[x_][y_] := {{Cos[x], I Sin[x]}, {I Sin[x], Cos[x]}}.y;
stepA[a_][l_] := Flatten[evo[a] /@ Partition[l, 2, 2, 1]];   
stepB[a_][l_] :=     RotateRight[Flatten[evo[a] /@ Partition[RotateLeft[l], 2, 2, 1]]];   
step[a_][l_] := stepB[a][stepA[a][l]]   )]

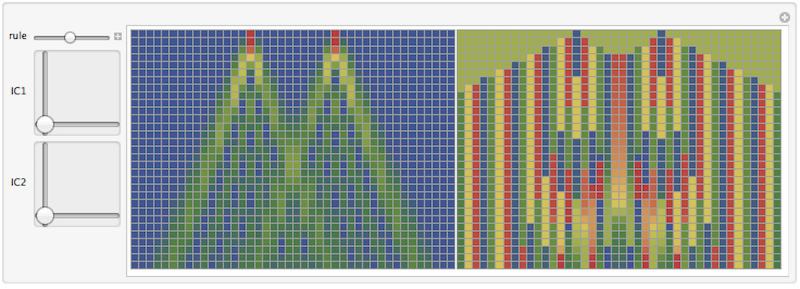
The two plots are amplitude and phase of the evolution. Now let’s verify that evolution is indeed unitary. Variable data (the evolution steps) is global so we could just simply apply:
Tr[Abs[#]^2] & /@ data
(* Out[] = {0.0325, 0.0325, 0.0325, ..... } *)
POSTED BY: Vitaliy Kaurov
2 Replies
Sort By:
Thank you for catching this. I added the definition for the evo function in the Initialization section of Manipulate.
POSTED BY: Vitaliy Kaurov
Dear Vitaliy,

Thank you very much for sharing this! I am glad to see the hood popped on the Footnotes section, since the associated code corpus has a few gaps. I may be overlooking the definition, but is there any explicit declaration of evo? Thank you very much, Vitaliy!


Best,
Arjan 
POSTED BY: Arjan Puniani
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract