I am not certain I understand what you wish to plot. Perhaps this will help

In[1]:= sols = Table[x /. DSolve[{x'[t] - 1 - r*x[t] - x[t]^2 == 0, x[0] == 0}, x, t][[1, 1]], {r, 1, 3}]

During evaluation of In[1]:= Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. >>

During evaluation of In[1]:= Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. >>

Out[1]= {
 Function[{t}, 1/2 (-1 + Sqrt[3] Tan[1/2 (\[Pi]/3 + Sqrt[3] t)])], 
 Function[{t}, -(t/(-1 + t))], 
 Function[{t}, -(((-3 + Sqrt[5]) (-1 + E^(Sqrt[5] t)))/(2 - 7 E^(Sqrt[5] t) + 3 Sqrt[5] E^(Sqrt[5] t)))]
}

Then perhaps you can do something like this

Table[ParametricPlot[Evaluate[{sols[[r]][t], D[sols[[r]][t], t]}], {t, 0, 100}], {r, 1, 3}]

or perhaps something like this

Show[Table[ParametricPlot[Evaluate[{sols[[r]][t], D[sols[[r]][t], t]}], {t, 0, 100}], {r, 1, 3}]]

I am uncertain whether these plots are precisely correct and you should study all these results very carefully to make certain that there are no errors.

You might want to be cautious with your numerical solution.

Clear[x]; r = 1; eqn = x'[t] - 1 - r*x[t] - x[t]^2 == 0;
sol = x /. NDSolve[{eqn, x[0] == 0}, x, {t, 0, 100}][[1, 1]];

NDSolve::ndsz: At t == 1.2091994106422708`, step size is effectively zero; singularity or stiff system suspected. >>

And

ParametricPlot[Evaluate[{sol[t], D[sol[t], t]}], {t, 0, 100}]

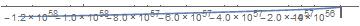
And

Plot[sol[t], {t, 0, 100}]

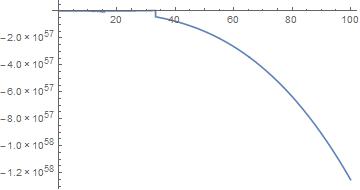
But

Clear[x]; r = 1; eqn = x'[t] - 1 - r*x[t] - x[t]^2 == 0;
sol = x /. DSolve[{eqn, x[0] == 0}, x, t][[1, 1]];

Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. >>

And

ParametricPlot[Evaluate[{sol[t], D[sol[t], t]}], {t, 0, 100}]

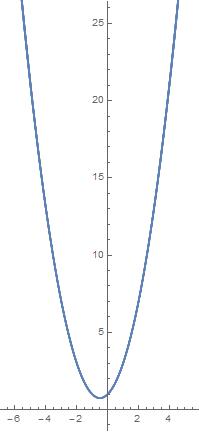
And

Plot[sol[t], {t, 0, 100}]

And

In[11]:= sol

Out[11]= Function[{t}, 1/2 (-1 + Sqrt[3] Tan[1/6 (\[Pi] + 3 Sqrt[3] t)])]

Those warning messages are often there for a very good reason.

Even the warning about using Reduce is there for a good reason. Unfortunately it does not include a link to, and I have never been able to track down, a brilliantly well written paragraph in the documentation that describes exactly what that intends you to do.

Your equation is malformed. This variation works:
eqn = x'[t] - 1 - r*x[t] - x[t]^2 == 0