In order to contextualize the question, let us first examine some examples. Function Nest is useful to generate the multiple compositions of a given function:
NestList[f, x, 5]
{x, f[x], f[f[x]], f[f[f[x]]], f[f[f[f[x]]]], f[f[f[f[f[x]]]]]}
For instance, if f (x) = 2 x + 1
Simplify[NestList[2 # + 1 &, x, 5]]
{x, 1 + 2 x, 3 + 4 x, 7 + 8 x, 15 + 16 x, 31 + 32 x}
Given the equation f (f (x)) = a x + b, with a > 0 its solution can be readily verified to be:
Simplify[Sqrt[a] x + b/(1 + Sqrt[a]) /. x -> Sqrt[a] x + b/(1 + Sqrt[a])]
b + a x
or alternatively :
Simplify[Nest[Sqrt[a] # + b/(1 + Sqrt[a]) &, x, 2], a > 0]
b + a x
To obtain the solution to f (f (f (x))) = a x + b we use Reduce
Reduce[Nest[c # + d &, x, 3] == a x + b, {x}]
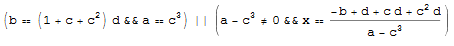
and verify the answer
FullSimplify[
Nest[(Power[a, (3)^-1] # + b/(
1 + Power[a, (3)^-1] + Power[a^2, (3)^-1])) &, x, 3], a > 0]
b + a x
Now let us consider quadratic equations. Consider solving the equation f (f (x)) = x^2. Martin Gardner solved it a while ago but do not look it up!. It would be worthwhile the time you spend in trying to solve it.
After you have solved it, consider now the equation f (f (x)) = x^2 + 1.
How can we solve it? Do we need to consider the complex domain, that is f (f (z)) = z^2 + 1? Do we have to resort to numerical methods, at least to have an idea of what it looks like? If so, I would still be interested.