Group Abstract

Message Boards

WOLFRAM COMMUNITY

5.5K Views

3 Replies

1 Total Like

View groups...

Follow this post

Share this post:

GROUPS:

Graphics and Visualization Optimization

Circumscribing a Quartic Curve

Frank Kampas

Frank Kampas, Physicist at Large Consulting

Posted 10 years ago

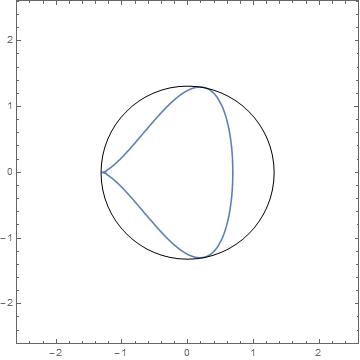
Suppose I want to find the smallest circle, centered at the origin, which circumscribes a Piriform curve ( http://mathworld.wolfram.com/PiriformCurve.html ), defined by piri[ { x, y} ] == 0 where piri[{x_, y_}] = x^3 (2 - x) - y^2; by shifting the curve's center along the x-axis. This involves minimizing the maximum distance from the origin to the shifted curve. The maximum distance as a function of the shift can be calculated as follows: f[x0_] = MaxValue[{Sqrt[x^2 + y^2], piri[{x - x0, y}] == 0}, {x, y}]; The result is a Piecewise function containing Root functions and cannot be analytically minimized, but is equal to -x0 for x0 <= 1/27 (-17 - 7 Sqrt[7]) and larger values for x0 greater than that value, as shown in the following plot Plot[f[x0], {x0, -2, 0}] 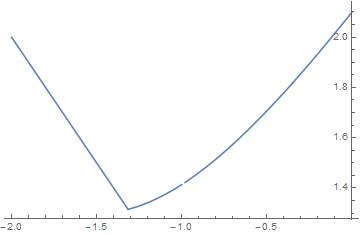Therefore the minimization is obtained at that value (approximately -1.3) The result can be visualized as Show[ContourPlot[ piri[{x - 1/27 (-17 - 7 Sqrt[7]), y}] == 0, {x, -2.5, 2.5}, {y, -2.5, 2.5}], Graphics @ Circle[{0, 0}, 1/27 (-17 - 7 Sqrt[7])]]

POSTED BY: Frank Kampas

3 Replies

Sort By:

Udo Krause

Udo Krause, NOrganization

Posted 10 years ago

Another approach; define In[85]:= Clear[\[ScriptCapitalR]] With[{a = 2, b = 3}, \[ScriptCapitalR] = ImplicitRegion[ a^4 y^2 - b^2 x^3 (2 a - x) < 0, {x, y}] ] Out[86]= ImplicitRegion[-9 (4 - x) x^3 + 16 y^2 < 0, {x, y}] In[77]:= Clear[f] f[a_?NumericQ, b_?NumericQ, z_?NumericQ] := Length[ FindInstance[a^4 y^2 - b^2 x^3 (2 a - x) == 0 && (x - z)^2 + y^2 - z^2 == 0, {x, y}, Reals, 8] ] /; UnsameQ[x, z] && UnsameQ[y, z] and plot RegionPlot[{\[ScriptCapitalR], Disk[{x, 0}, x] /. x -> NIntegrate[Boole[f[2, 3, z] > 1], {z, 0, 5}]}] No error messages anymore, but one has to choose two constants: an upper bound for the intersections and an upper bound for the numerical integration which has the only purpose to find out the jumping point from 5 intersections through 3 into 1 intersection.

Another approach; define

    In[85]:= Clear[\[ScriptCapitalR]]
     With[{a = 2, b = 3},
       \[ScriptCapitalR] = ImplicitRegion[ a^4  y^2 - b^2 x^3 (2 a - x) < 0, {x, y}]
     ]
    Out[86]= ImplicitRegion[-9 (4 - x) x^3 + 16 y^2 < 0, {x, y}]

    In[77]:= Clear[f]
    f[a_?NumericQ, b_?NumericQ, z_?NumericQ] := Length[
       FindInstance[a^4  y^2 - b^2 x^3 (2 a - x) == 0 && (x - z)^2 + y^2 - z^2 == 0, {x, y}, Reals, 8]
     ] /; UnsameQ[x, z] && UnsameQ[y, z]

and plot

RegionPlot[{\[ScriptCapitalR], Disk[{x, 0}, x] /. x -> NIntegrate[Boole[f[2, 3, z] > 1], {z, 0, 5}]}]

enter image description here

No error messages anymore, but one has to choose two constants: an upper bound for the intersections and an upper bound for the numerical integration which has the only purpose to find out the jumping point from 5 intersections through 3 into 1 intersection.

POSTED BY: Udo Krause

Frank Kampas

Frank Kampas, Physicist at Large Consulting

Posted 10 years ago

That's an interesting approach. I've been trying to define a constraint for ellipse packing that prevents their overlap, but it didn't occur to me to use the area of the region intersection.

POSTED BY: Frank Kampas

Udo Krause

Udo Krause, NOrganization

Posted 10 years ago

State e.g. In[120]:= Clear[\[ScriptCapitalR]] With[{a = 2, b = 3}, \[ScriptCapitalR] = ImplicitRegion[ a^4 y^2 - b^2 x^3 (2 a - x) < 0, {x, y}] ] Out[121]= ImplicitRegion[-9 (4 - x) x^3 + 16 y^2 < 0, {x, y}] and give it to `FindRoot` In[162]:= FindRoot[Area[RegionIntersection[\[ScriptCapitalR], Disk[{x, 0}, x]]] - Area[\[ScriptCapitalR]], {x, 1, 0, 6}] During evaluation of In[162]:= Area::nmet: Unable to compute the area of region RegionIntersection[Disk[{x,0},x],ImplicitRegion[-9 (4-x) x^3+16 y^2<0,{x,y}]]. >> During evaluation of In[162]:= FindRoot::jsing: Encountered a singular Jacobian at the point {x} = {4.05281}. Try perturbing the initial point(s). >> Out[162]= {x -> 4.05281} In[163]:= RegionPlot[{\[ScriptCapitalR], Disk[{x, 0}, x] /. %} ] the function is not ideal for `FindRoot` because it becomes constant zero for $x$ equal to or greater than the searched $x$ and `FindRoot` complains about that, nevertheless

State e.g.

In[120]:= Clear[\[ScriptCapitalR]]
With[{a = 2, b = 3},
 \[ScriptCapitalR] = ImplicitRegion[ a^4  y^2 - b^2 x^3 (2 a - x) < 0, {x, y}]
 ]
Out[121]= ImplicitRegion[-9 (4 - x) x^3 + 16 y^2 < 0, {x, y}]

and give it to FindRoot

In[162]:= FindRoot[Area[RegionIntersection[\[ScriptCapitalR], Disk[{x, 0}, x]]] - Area[\[ScriptCapitalR]], {x, 1, 0, 6}]
During evaluation of In[162]:= Area::nmet: Unable to compute the area of region RegionIntersection[Disk[{x,0},x],ImplicitRegion[-9 (4-x) x^3+16 y^2<0,{x,y}]]. >>
During evaluation of In[162]:= FindRoot::jsing: Encountered a singular Jacobian at the point {x} = {4.05281}. Try perturbing the initial point(s). >>
Out[162]= {x -> 4.05281}

In[163]:= RegionPlot[{\[ScriptCapitalR], Disk[{x, 0}, x] /. %} ]

the function is not ideal for FindRoot because it becomes constant zero for $x$ equal to or greater than the searched $x$ and FindRoot complains about that, nevertheless

enter image description here

POSTED BY: Udo Krause

Reply to this discussion

Reply Preview

Attachments

Remove Add a file to this post

Follow this discussion

or Discard

Feedback