In 1997, the following problem was posed to test a programme. How many different 4 x4 matrices having nonnegative integer entries have row sums
1000, 9000, 3000, 440
and column sums
2000, 4000, 200, 7240 ?
The answer is exactly 160256589785681535184841, and it was found in 2 seconds real time on a typical workstation at MSRI, Berkeley, in 1997!. How did they came up with that number so rapidly?
The following is one of those matrices
Timing[MatrixForm[{{x1, x2, x3, x4}, {x5, x6, x7, x8}, {x9, x10, x11,
x12}, {x13, x14, x15, x16}} /.
First@FindInstance[(x1 + x2 + x3 + x4 ==
1000) && (x5 + x6 + x7 + x8 ==
9000) && (x9 + x10 + x11 + x12 ==
3000) && (x13 + x14 + x15 + x16 ==
440) && (x1 + x5 + x9 + x13 ==
2000) && (x2 + x6 + x10 + x14 ==
4000) && (x3 + x7 + x11 + x15 ==
200) && (x4 + x8 + x12 + x16 == 7240) && x1 >= 0 && x2 >= 0 &&
x3 >= 0 && x4 >= 0 && x5 >= 0 && x6 >= 0 && x7 >= 0 &&
x8 >= 0 && x9 >= 0 && x10 >= 0 && x11 >= 0 && x12 >= 0 &&
x13 >= 0 && x14 >= 0 && x15 >= 0 && x16 >= 0, {x1, x2, x3, x4,
x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15, x16},
Integers]]]

if we divide all the sums by 40 (which is the gcd of the given sums) we get the following example
Timing[MatrixForm[{{x1, x2, x3, x4}, {x5, x6, x7, x8}, {x9, x10, x11,
x12}, {x13, x14, x15, x16}} /.
First@FindInstance[(x1 + x2 + x3 + x4 ==
25) && (x5 + x6 + x7 + x8 == 225) && (x9 + x10 + x11 + x12 ==
75) && (x13 + x14 + x15 + x16 == 11) && (x1 + x5 + x9 + x13 ==
50) && (x2 + x6 + x10 + x14 ==
100) && (x3 + x7 + x11 + x15 == 5) && (x4 + x8 + x12 + x16 ==
181) && x1 >= 0 && x2 >= 0 && x3 >= 0 && x4 >= 0 && x5 >= 0 &&
x6 >= 0 && x7 >= 0 && x8 >= 0 && x9 >= 0 && x10 >= 0 &&
x11 >= 0 && x12 >= 0 && x13 >= 0 && x14 >= 0 && x15 >= 0 &&
x16 >= 0, {x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12,
x13, x14, x15, x16}, Integers]]]

Note this solution is not the previous one divided by 40.
In looking for a matrix having the first row adding to 25, the above row {0, 22, 0, 3} must be among the following 3276
FrobeniusSolve[{1, 1, 1, 1}, 25]
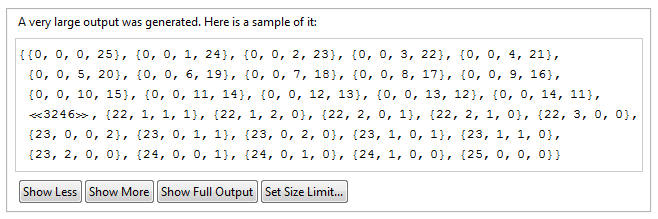
and there are 1949476 for the second row adding to 225. There is no need to generate all solutions to know how many are there, we know that, in general, the number of solutions to the Diophantine equation
x1 + x2 + x3 + x4 = n , x1, x2, x3, x4 integer values >= 0
is Binomial[n + 3, n] so, in orther to test all rows complying with their sums to see whether they comply with the sum of the columns as well we need to examine
Times @@ (Binomial[# + 3, #] & /@ {1000, 9000, 3000, 440})
1322852284046903937703609378206302241
cases to end up with the amount quoted at the beginning. A massive task. So, again, how did they do it ?.
As I do not know the answer, I thought I could explain something to give an idea of what is involved by examining the complexities of an easier problem. Let H (n, r) denote the number of square matrices n x n with non - negative elements wherein each row and column sum is equal to r.
It is easy to see that H (2, r) = r + 1.
The problem to compute H (n, r) goes back to McMahon (1916) who showed that H (3, r) is equal to Binomial(r+2, 2)+3 Binomial(r+3, 4). This quantity grows as:
Table[Binomial[r + 2, 2] + 3 Binomial[r + 3, 4], {r, 20}]
{6, 21, 55, 120, 231, 406, 666, 1035, 1540, 2211, 3081, 4186, 5565, 7260, 9316, 11781, 14706, 18145, 22155, 26796}
The 21 above corresponds to the number of elements in the following list
MatrixForm /@ ({{x1, x2, x3}, {x4, x5, x6}, {x7, x8, x9}} /.
Solve[(x1 + x2 + x3 == x4 + x5 + x6 == x7 + x8 + x9 ==
x1 + x4 + x7 == x2 + x5 + x8 == x3 + x6 + x9 == 2) && x1 >= 0 &&
x2 >= 0 && x3 >= 0 && x4 >= 0 && x5 >= 0 && x6 >= 0 && x7 >= 0 &&
x8 >= 0 && x9 >= 0, {x1, x2, x3, x4, x5, x6, x7, x8, x9},
Integers])
Length[%]

by the way, the 9316 includes magic squares . if one wants to find out how many magic squares 3 x3 are there (disregarding equivalent ones under rotation/reflections), a better method is the following
MatrixForm[Partition[#, 3]] & /@
Select[Permutations[
Range[9]], ({{x1, x2, x3}, {x4, x5, x6}, {x7, x8, x9}} =
Partition[#,
3]; (x1 + x2 + x3 == x4 + x5 + x6 == x7 + x8 + x9 ==
x1 + x4 + x7 == x2 + x5 + x8 == x3 + x6 + x9 == 15) && (x1 ==
Min[x1, x3, x7, x9]) && (x3 < x7)) &]

What could be the formula for H (4, r)?. Stanley and Ehrhart showed that H (n, r) is a polynomial in r of degree (n - 1)^2. For example, H (3, r) is
Simplify[Binomial[r + 2, 2] + 3 Binomial[r + 3, 4]]
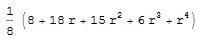
To obtain the expression for H(4,r) we proceed by interpolating the following values.
Timing[Table[
Length[({{x1, x2, x3, x4}, {x5, x6, x7, x8}, {x9, x10, x11,
x12}, {x13, x14, x15, x16}} /.
Solve[(x1 + x2 + x3 + x4 == x5 + x6 + x7 + x8 ==
x9 + x10 + x11 + x12 == x13 + x14 + x15 + x16 ==
x1 + x5 + x9 + x13 == x2 + x6 + x10 + x14 ==
x3 + x7 + x11 + x15 == x4 + x8 + x12 + x16 == i) && x1 >= 0 &&
x2 >= 0 && x3 >= 0 && x4 >= 0 && x5 >= 0 && x6 >= 0 &&
x7 >= 0 && x8 >= 0 && x9 >= 0 && x10 >= 0 && x11 >= 0 &&
x12 >= 0 && x13 >= 0 && x14 >= 0 && x15 >= 0 && x16 >= 0, {x1,
x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15,
x16}, Integers])], {i, 0, 8}]]
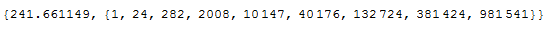
and the answer for H (4, r) is
Expand[InterpolatingPolynomial[{{0, 1}, {1, 24}, {2, 282}, {3,
2008}, {4, 10147}, {5, 40176}, {6, 132724}, {7, 381424}, {8,
981541}}, r]]
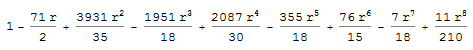
To date not even H (7, r) is known.