Hi Bryan,
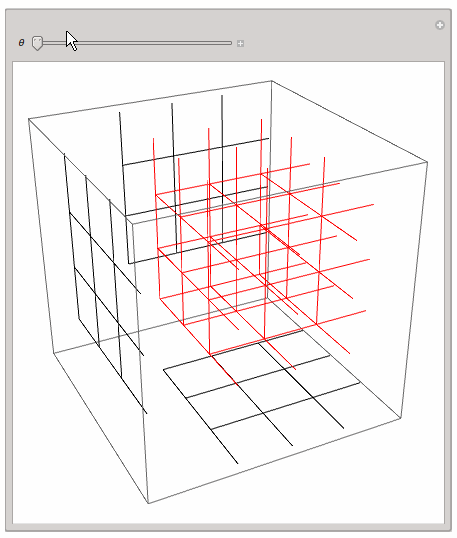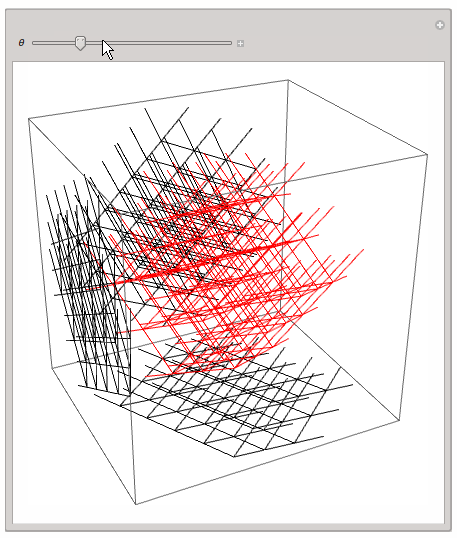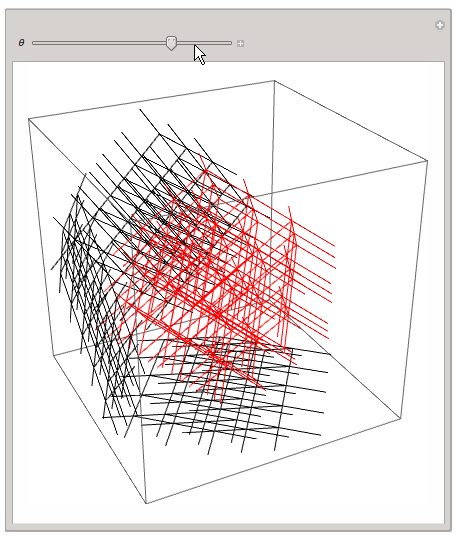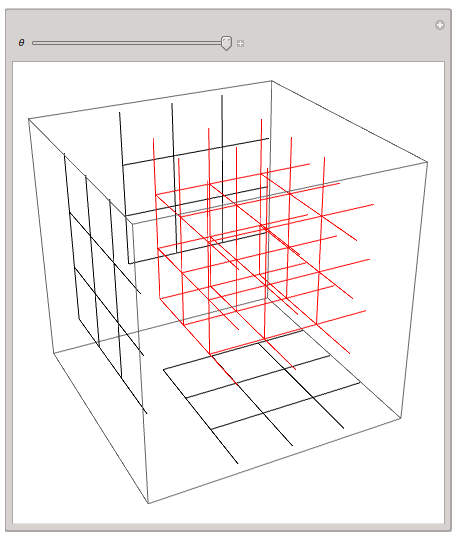
a while ago I was playing around with the same idea. I found the 3D or 2D projection of a 4D lattice quite instructive. Here is my code; it should be self explaining:
ClearAll["Global`*"]
(rot4D = RotationMatrix[\[Theta], {{1, 0, 0, 0}, {1, 1, 1, 1}}]) // MatrixForm
nmax = 1;
points4D = Flatten[Table[{
{{x, y, z, t}, {x + 1, y, z, t}},
{{x, y, z, t}, {x, y + 1, z, t}},
{{x, y, z, t}, {x, y, z + 1, t}},
{{x, y, z, t}, {x, y, z, t + 1}}},
{x, -nmax, nmax}, {y, -nmax, nmax}, {z, -nmax, nmax}, {t, -nmax,
nmax}], 5];
rotStruct4D[\[Theta]_] = {Red,
Line /@ Partition[{#1, #2, #3} & @@@ (rot4D.# & /@ points4D), 2]};
rotStruct4Dx[\[Theta]_] = {Black, Line /@
Partition[{-2.5 nmax, 0, 0} + {0, 1, 1} # & /@ ({#1, #2, #3} & @@@ (rot4D.# & /@ points4D)), 2]};
rotStruct4Dy[\[Theta]_] = {Black, Line /@
Partition[{0, -2.5 nmax, 0} + {1, 0, 1} # & /@ ({#1, #2, #3} & @@@ (rot4D.# & /@ points4D)), 2]};
rotStruct4Dz[\[Theta]_] = {Black, Line /@
Partition[{0, 0, -2.5 nmax} + {1, 1, 0} # & /@ ({#1, #2, #3} & @@@ (rot4D.# & /@ points4D)), 2]};
Manipulate[Graphics3D[{rotStruct4D[\[Theta]], rotStruct4Dx[\[Theta]], rotStruct4Dy[\[Theta]], rotStruct4Dz[\[Theta]]},
ImageSize -> 600], {\[Theta], 0, 2 Pi}]
This - of course! - is very simple and rotates the lattice only in a single hyperplane, but one can get a first impression.
Regards -- Henrik