Hi math,
There are a number of syntax errors you will find corrected below. (Look up FindFit in the help system!)
Best, David
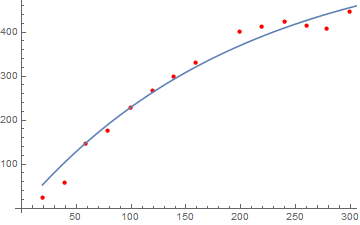
In[1]:= xData = {19.38, 39.36, 58.62, 78.6, 99, 119.4, 138.6, 158.4,
199.2, 219, 239.4, 259.8, 278.4, 299.4}; yData = {23.1667, 59.1667,
147, 176.667, 228.333, 266.667, 300, 330, 401.667, 413.333, 425,
415, 408.333, 446.667};
In[2]:= (* FindFit wants pairs *)
data = Transpose@{xData, yData};
In[3]:= (* the model is an expression for the dependent variable in \
terms of the independent and parameters. Note the space in b x, and \
also the curly braces for lists *)
solution = FindFit[data, (a/b)*(1 - E^(-b x)), {a, b}, x]
Out[3]= {a -> 2.91944, b -> 0.00494724}
In[4]:= Show[ListPlot[data, PlotStyle -> Red],
Plot[(a/b)*(1 - E^(-b x)) /. solution, {x, 19, 450}]]
 Attachments:
Attachments: