Hi Peter,

you posted the very same question two month ago and - as far as I can see - a concise answer was given. If you do not want the to see the rotated axes, then just add Axes->False to the plot options inside the epilog (giving the same answer a second time):

pArgs = Sequence[{x, -2, 2}, PlotRange -> {-3, 3}, ImageSize -> 500];
Plot[x, Evaluate@pArgs, PlotStyle -> {Opacity[0]}, 
 Epilog -> Inset[Rotate[Plot[x^2, Evaluate@pArgs, Axes -> False], -20 Degree]]]

But if you need not a graphical but a more mathematical approach you can regard any function as a parametric space curve and rotate this:

rotmat[a_] := {{Cos[a], Sin[a]}, {-Sin[a], Cos[a]}}
f[x_] := x^2
ParametricPlot[rotmat[20 \[Degree]].{t, f[t]}, {t, -2, 2}]

Regards -- Henrik

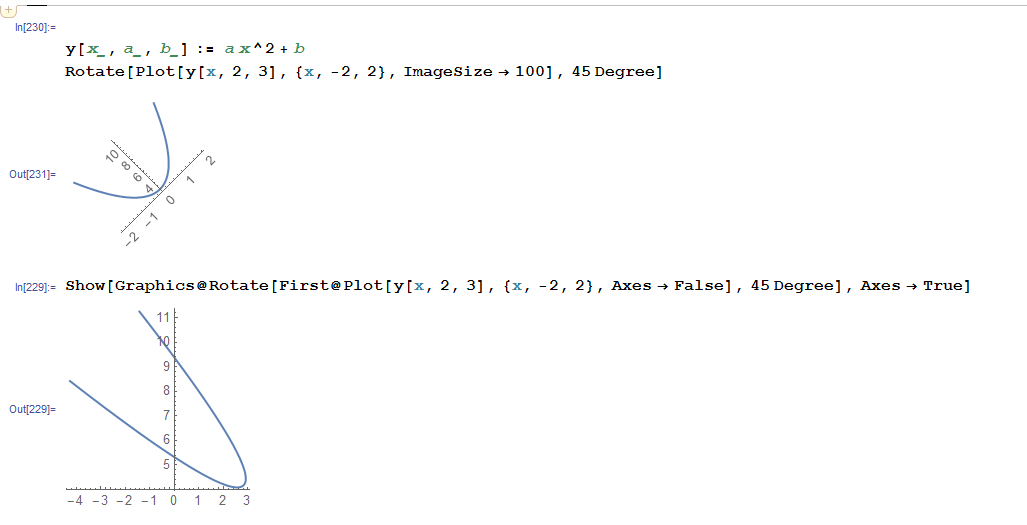
One normally rotates a coordinates frames. But you can achieve what you want like this

Replace

y[x_, a_, b_] := a x^2 + b
Rotate[Plot[y[x, 2, 3], {x, -2, 2}], 45 Degree]

with

Show[Graphics@
  Rotate[First@Plot[y[x, 2, 3], {x, -2, 2}, Axes -> False], 
   45 Degree], Axes -> True]

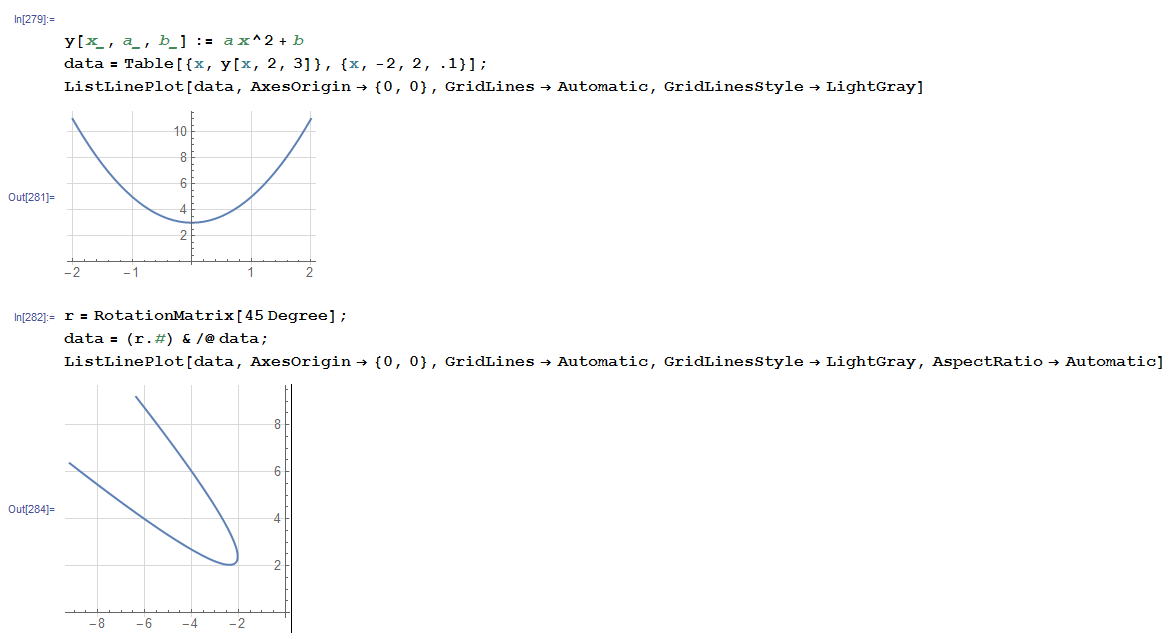
Another (better?) option is to obtain the data itself (position vector of each point) and apply a RotationMatrix to each point. Something like

y[x_, a_, b_] := a x^2 + b
data = Table[{x, y[x, 2, 3]}, {x, -2, 2, .1}];
ListLinePlot[data, AxesOrigin -> {0, 0}, GridLines -> Automatic,  GridLinesStyle -> LightGray]

r = RotationMatrix[45 Degree];
data = (r.#) & /@ data;
ListLinePlot[data, AxesOrigin -> {0, 0}, GridLines -> Automatic, GridLinesStyle -> LightGray, AspectRatio -> Automatic]