Welcome to the Wolfram Community, Jack. Please in future follow the following rules:

• Read basic tips of this forum

• Show what you have tried first - meaning show your CODE - there is a lot of documentation on differential equations and I am sure you could easily adopt those if you invest some time in reading

• Search internet if anything was already done on the subject

• Do not post images with a lot of formulas - people tend to ignore that, explain clearly in your own words what do you need - and again post your CODE at least trying to read documentation

Because this is your 1st post, I would give you some references. There is a notebook attached to this post "Numerical solution of the Falkner-Skan equation for various wedge angles" Housam Binous with discription:

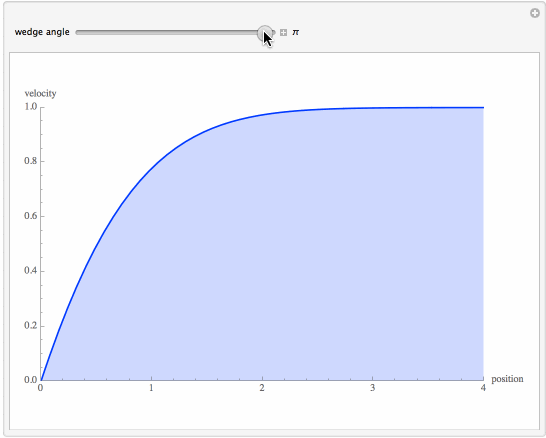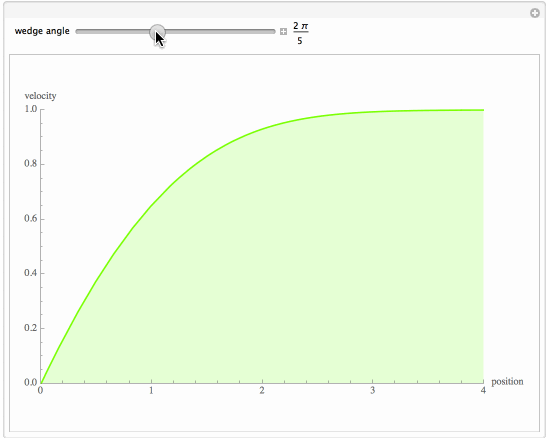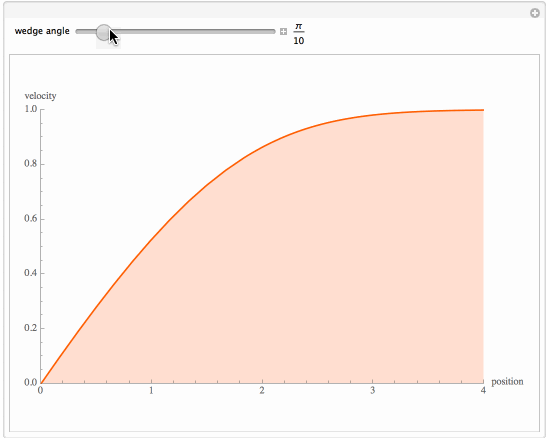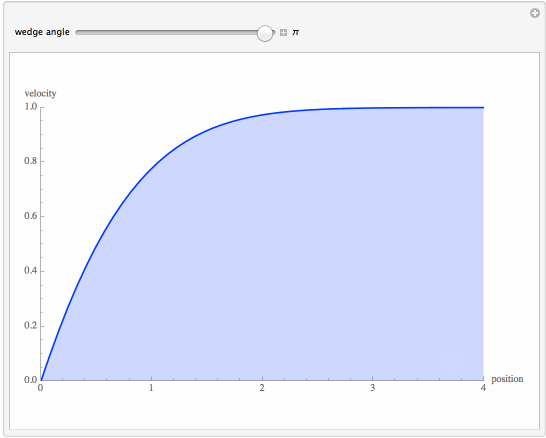
Flow past a wedge is governed by the Falkner-Skan equation. This equation admits only numerical solution, which requires the application of the shooting technique. The notebook plots the velocity for various wedge angles. The result obtained is in agreement with figure 8-10 in page 352 of Deen's book (Analysis of Transport Phenomena, William M. Deen, OUP, 1998). The well-known Blasius equation appears as a particular case in this study. It represents the flow past a flat plate (parameter beta=0, or a wedge angle equal to zero). Planar stagnation flow is also treated by the notebook (parameter beta=1 or a wedge angle equal to Pi).

Housam Binous also published a demonstration with minimal code:

Numerical Solution of the Falkner-Skan Equation for Various Wedge Angles

Manipulate[Module[{plt, sol, DFEnd, SOL1, plt1}, 
  sol[\[Xi]_] := NDSolve[{D[f[\[Eta]], {\[Eta], 3}] + 
       f[\[Eta]] f''[\[Eta]] + \[Beta]/\[Pi] (1 - (f'[\[Eta]])^2) == 0, f[0] == 0, f'[0] == 0, 
     f''[0] == \[Xi]}, {f[\[Eta]]}, {\[Eta], 0, 5}, MaxSteps -> Infinity];
  DFEnd[\[Xi]_?NumericQ] := D[f[\[Eta]] /. sol[\[Xi]], {\[Eta], 1}] /. \[Eta] -> 4;
  SOL1 = FindRoot[DFEnd[\[Xi]] == 1, {\[Xi], 1.2}]; 
  plt1 = Plot[Evaluate[D[f[\[Eta]] /. sol[\[Xi] /. SOL1], {\[Eta], 1}]], {\[Eta], 0, 4}, 
    PlotStyle -> Hue[\[Beta]/5], PlotRange -> {{0, 4}, {0, 1}}, 
    AxesLabel -> {"position", "velocity"}, ImageSize -> {500, 350}]],
 {{\[Beta], 0, "wedge angle"}, 0, \[Pi], \[Pi]/10, Appearance -> "Labeled"},
 TrackedSymbols :> {\[Beta]}]

Attachments: