Message Boards Message Boards

13
|
18524 Views
|
8 Replies
|
28 Total Likes
View groups...
Share
Share this post:

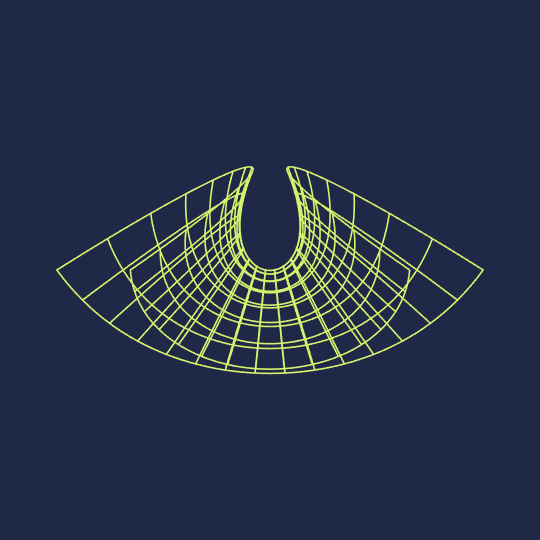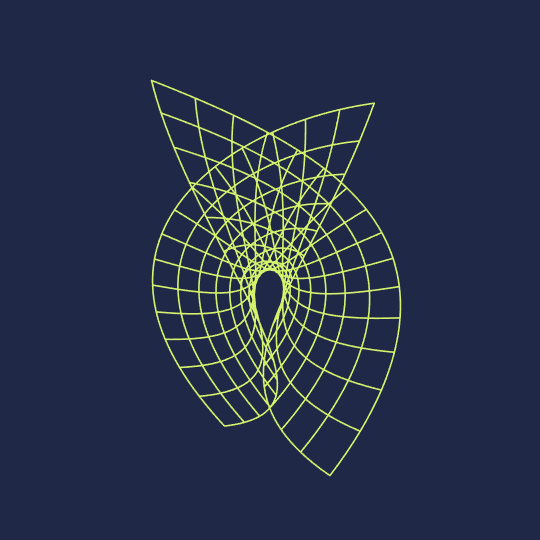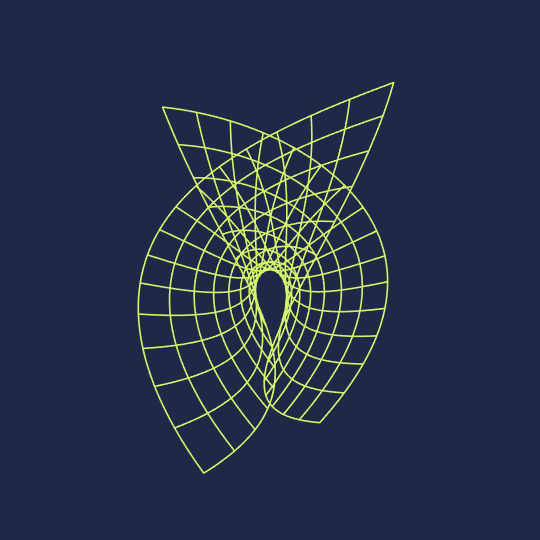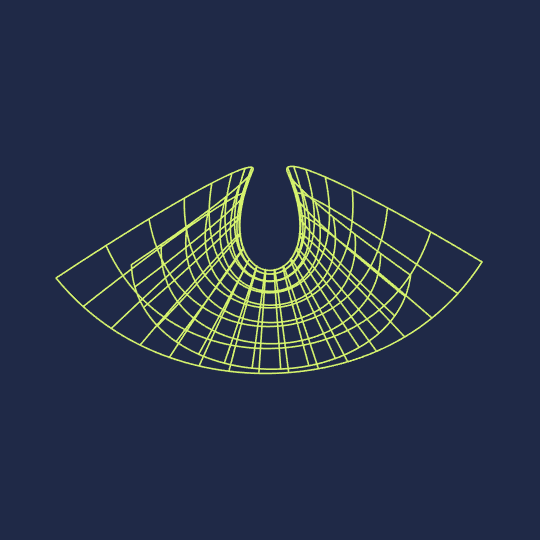
[GIF] Enneper surface + an introduction

Enneper surface

Hello, Wolfram Community. My name is Clayton Shonkwiler, and I'm a mathematician at Colorado State University, primarily interested in moduli spaces of random walks. I also make animated GIFs using Mathematica; you can see my latest above. My website is at shonkwiler.org and I post my GIFs to Tumblr, Ello, and Twitter (as well as posting stills to Instagram) if you'd like to follow me in one of those places. If there's interest I would also like to start posting my GIFs along with source code here, as I'd be very happy to get feedback.

As for the code for the above GIF, first is a function which transforms hex color values into RGB:

RGBFromHex[hex_] := RGBColor[(FromDigits[#, 16] & /@ StringPartition[hex, 2])/255]

I use this quite a bit, but I don't really like it; is there a better way to do this? A built-in function would be ideal.

Anyway, here's the code for the associated family of the Enneper surface and the Manipulate object corresponding to the above GIF (of course I originally did this by parametrically plotting the surface with PlotStyle->None and messing with MeshStyle, but creating tables of curves gives a cleaner final image):

Enneper[u_, v_, θ_] := Re[E^(I θ) {z - z^3/3, I z + I z^3/3, z^2} /. z -> u + I v]

Manipulate[
 Graphics3D[{RGBFromHex["d5f26d"], Thickness[.003], 
   Line[Table[Enneper[u, v, θ], {u, -3/2, 3/2, 1/5}, {v, -3/2, 3/2, 1/20}]], 
   Line[Table[Enneper[u, v, θ], {v, -3/2, 3/2, 1/5}, {u, -3/2, 3/2, 1/20}]]}, 
  PlotRange -> 4.5, ViewPoint -> Front, Boxed -> False, 
  Axes -> None, Background -> RGBFromHex["1f2947"], ImageSize -> 540], 
{θ, 0, 2 π}]
POSTED BY: Clayton Shonkwiler
8 Replies
Sort By:
J. M.
J. M.
Posted 9 years ago

Very nicely done! (Nice enough to make me delurk. ;) ) Please allow me to tweak things slightly:

(* adapted from http://mathematica.stackexchange.com/a/18506 *)
hexToRGB = RGBColor @@ (IntegerDigits[FromDigits[StringReplace[#, "#" -> ""], 16], 256, 3]/255.) &;

(* from http://mathematica.stackexchange.com/a/200 *)
antialias[g_, n_: 3] := ImageResize[Rasterize[g, "Image", ImageResolution -> n 72], Scaled[1/n]]

enneper[u_, v_, ?_] = ComplexExpand[With[{z = u + I v}, Re[Exp[I ?] {z - z^3/3, I z + I z^3/3, z^2}]],
                                    TargetFunctions -> {Re, Im}];

frames = Table[antialias[ParametricPlot3D[enneper[u, v, ?], {u, -3/2, 3/2}, {v, -3/2, 3/2},
                                          Axes -> None, Background -> hexToRGB["1f2947"], Boxed -> False,
                                          BoundaryStyle -> Directive[AbsoluteThickness[1], hexToRGB["d5f26d"]],
                                          Mesh -> 14, MeshStyle -> Directive[AbsoluteThickness[1], hexToRGB["d5f26d"]],
                                          PlotRange -> 4.5, PlotStyle -> None]],
                {?, 0, 2 ?, 2 ?/30}];

Export["enneper.gif", frames, AnimationRepetitions -> ?, "DisplayDurations" -> 1./20];

a flipping minimal surface is what it is
POSTED BY: J. M.

Oh wow, I never looked at it from the default viewpoint (I'd already changed to the front view before I switched from rendering the whole surface to just showing the mesh). Very cool!
POSTED BY: Clayton Shonkwiler

This viewpoint is even nicer! Look at the posts above, your hexToRGB["d5f26d"] can be replaced by RGBColor["#d5f26d"]
POSTED BY: Sander Huisman
J. M.
J. M.
Posted 9 years ago

Hello Sander, I'm aware of the new functionality in RGBColor[]; nevertheless, I elected to use what I used to have code that will work in earlier versions. In any case, it is straightforward to modify my code to use the new method. ;)
POSTED BY: J. M.
Kyle Martin
Kyle Martin, WOLFRAM
Posted 9 years ago

Very neat. I am looking forward to future contributions!
POSTED BY: Kyle Martin

This is very beautiful, thank you for sharing ! I love your choice of the colors for the background and the surface? What is your process of choosing colors for your GIFs?

BTW in Wolfram Language there is built-in way of conversion hexadecimal to RGB color. I think people tend to miss it because it is in the details section on RGBColor function:

enter image description here

So your code would work the same way with RGBColor["#d5f26d"] and RGBColor["#1f2947"]. I have also noticed that broken surface animated with some delay makes a beautiful visual too:

Enneper[u_, v_, ?_] := Re[E^(I ?) {z - z^3/3, I z + I z^3/3, z^2} /. z -> u + I v]

Manipulate[Graphics3D[{RGBColor["#d5f26d"], Thickness[.003], 
   Line[Table[Enneper[u, v, ?], {u, -3/2, 3/2, 1/5}, {v, -3/2, 3/2, 1/20}]], 
   Line[Table[Enneper[u, v, ? + Pi], {v, -3/2, 3/2, 1/5}, {u, -3/2, 3/2, 1/20}]]}, 
  PlotRange -> 4.5, ViewPoint -> Top, Boxed -> False, Axes -> None, 
  Background -> RGBColor["#1f2947"], ImageSize -> 540, ViewAngle -> .47],
 {?, 0, 2 ?}]

enter image description here

But I think my GIF is more aliased and jumpy, - do you have some special settings for Export ? I think you might be exporting to lossless PNGs and assembling the GIF in another software, or something like that?

POSTED BY: Marina Shchitova

I didn't know about the built-in hex input, I made functions similar to the one Clayton posted many many times! Thanks for pointing it out!

Edit: I see now that it is a 10.1 update, so it is actually quite new!
POSTED BY: Sander Huisman

This is very beautiful, thank you for sharing ! I love your choice of the colors for the background and the surface? What is your process of choosing colors for your GIFs?

I mostly just look for color palettes from the web. For example, lately I've been using Adobe Color, Swiss Style Color Picker, and especially Design Seeds quite a bit.

So your code would work the same way with RGBColor["#d5f26d"] and RGBColor["#1f2947"].

Okay, now I feel stupid, but that's exactly what I wanted. Thank you!

But I think my GIF is more aliased and jumpy, - do you have some special settings for Export ? I think you might be exporting to lossless PNGs and assembling the GIF in another software, or something like that?

I used to always complain to people that Mathematica's 3D graphics weren't antialiased and that I had to export at super-high resolutions and then resize in a photo editing program to get smooth 3D images...and then I discovered this setting:

Antialising Quality setting

Once I turned the quality all the way up, I didn't have to do anything special to export nice-looking, antialiased 3D graphics anymore.

I actually do export directly to GIF, but I usually use "DisplayDurations"->{1/24} or "DisplayDurations"->{1/30} in Export to get smoother animations. So, for example, the actual code I used to produce the GIF I posted above is:

Export[NotebookDirectory[] <> "enneper.gif", enneper, 
 "DisplayDurations" -> {1/30}]
POSTED BY: Clayton Shonkwiler
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract