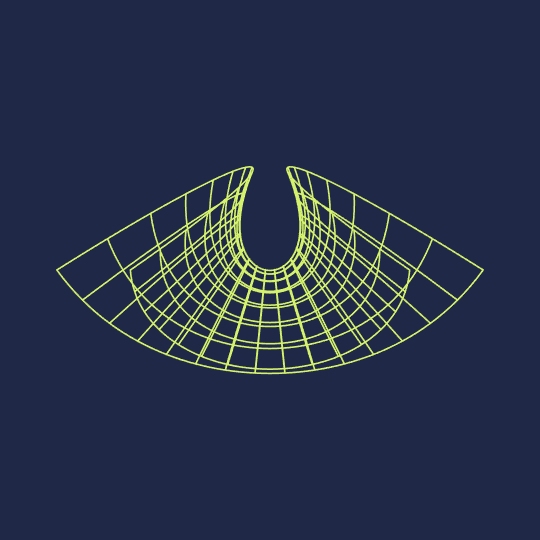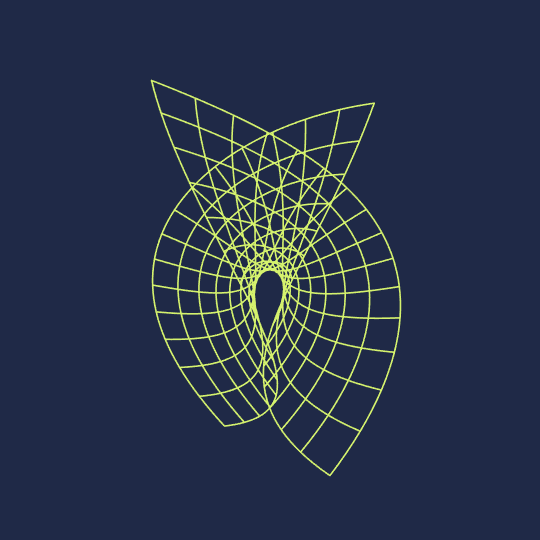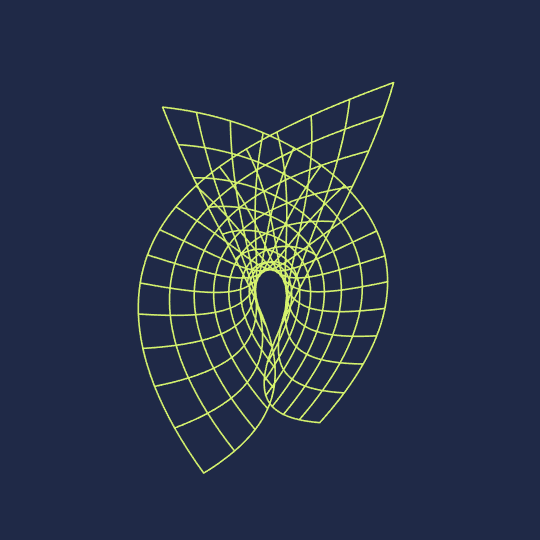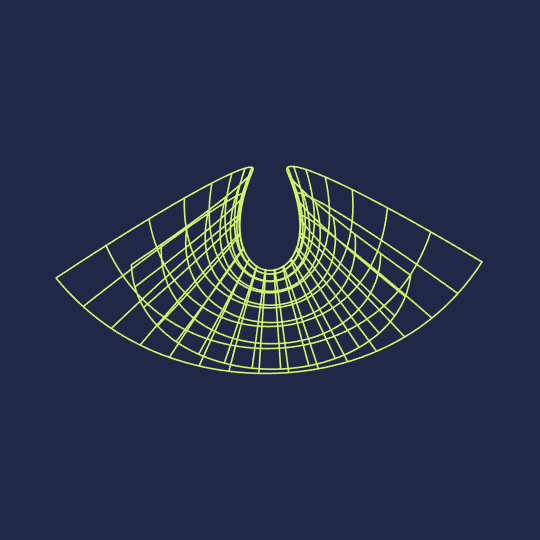
Hello, Wolfram Community. My name is Clayton Shonkwiler, and I'm a mathematician at Colorado State University, primarily interested in moduli spaces of random walks. I also make animated GIFs using Mathematica; you can see my latest above. My website is at shonkwiler.org and I post my GIFs to Tumblr, Ello, and Twitter (as well as posting stills to Instagram) if you'd like to follow me in one of those places. If there's interest I would also like to start posting my GIFs along with source code here, as I'd be very happy to get feedback.
As for the code for the above GIF, first is a function which transforms hex color values into RGB:
RGBFromHex[hex_] := RGBColor[(FromDigits[#, 16] & /@ StringPartition[hex, 2])/255]
I use this quite a bit, but I don't really like it; is there a better way to do this? A built-in function would be ideal.
Anyway, here's the code for the associated family of the Enneper surface and the Manipulate object corresponding to the above GIF (of course I originally did this by parametrically plotting the surface with PlotStyle->None and messing with MeshStyle, but creating tables of curves gives a cleaner final image):
Enneper[u_, v_, θ_] := Re[E^(I θ) {z - z^3/3, I z + I z^3/3, z^2} /. z -> u + I v]
Manipulate[
Graphics3D[{RGBFromHex["d5f26d"], Thickness[.003],
Line[Table[Enneper[u, v, θ], {u, -3/2, 3/2, 1/5}, {v, -3/2, 3/2, 1/20}]],
Line[Table[Enneper[u, v, θ], {v, -3/2, 3/2, 1/5}, {u, -3/2, 3/2, 1/20}]]},
PlotRange -> 4.5, ViewPoint -> Front, Boxed -> False,
Axes -> None, Background -> RGBFromHex["1f2947"], ImageSize -> 540],
{θ, 0, 2 π}]