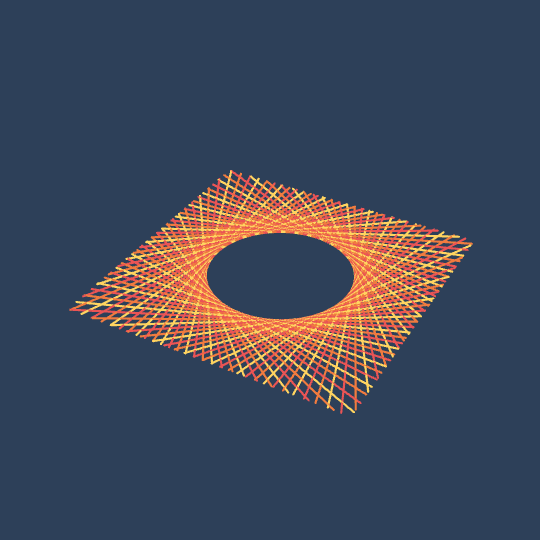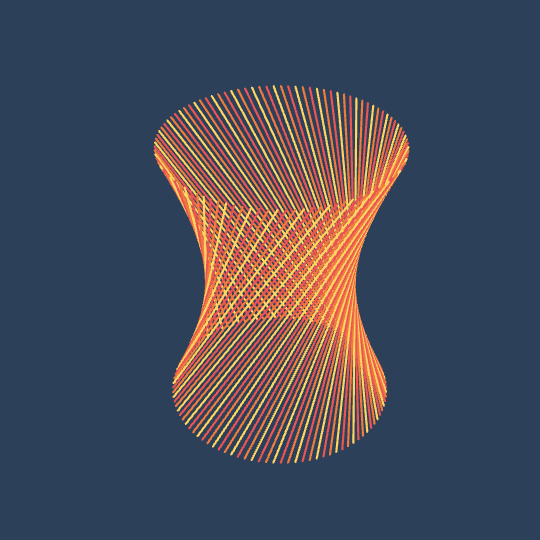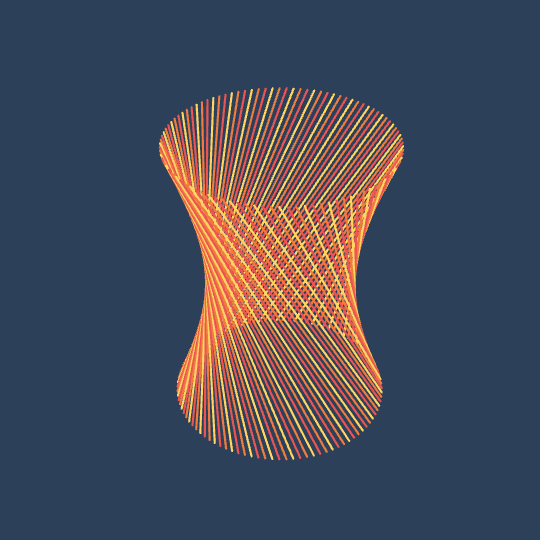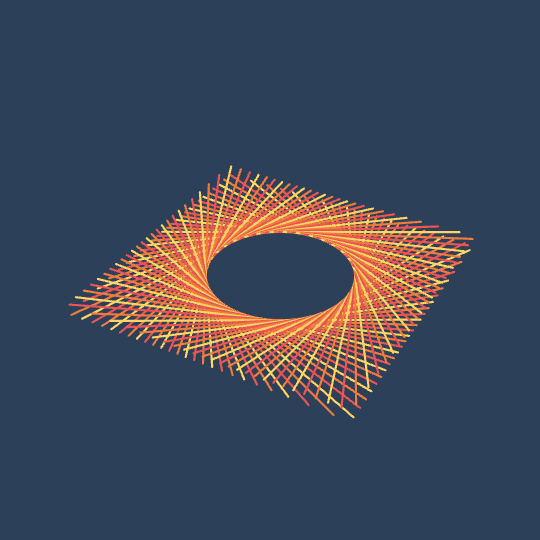
Ruled
I made this for this month's MCCC. The theme is "lines", which immediately made me think about ruled surfaces, so this is just a family of ruled hyperboloids.
Here's the code for the corresponding Manipulate[]:
MCCCcols2 = {RGBColor["#F07B3F"], RGBColor["#FFD460"],
RGBColor["#EA5455"], RGBColor["#2D4059"]}
Module[{n},
n = 99;
Manipulate[
Graphics3D[{Thickness[.004],
Table[{MCCCcols2[[Mod[t, 3, 1]]],
InfiniteLine[{{Cos[2 \[Pi] t/n], Sin[2 \[Pi] t/n],
0}, {Cos[2 \[Pi] t/n], Sin[2 \[Pi] t/n],
0} + {-Cos[\[Theta]] Sin[2 \[Pi] t/n],
Cos[\[Theta]] Cos[2 \[Pi] t/n], Sin[\[Theta]]}}]}, {t, 1,
n}]}, PlotRange -> 2, Boxed -> False, ImageSize -> 540,
ViewAngle -> \[Pi]/6, ViewCenter -> {.46, .5, 1/2},
Background -> MCCCcols2[[4]]], {\[Theta], 0, \[Pi]}]
]
The fact that the hyperboloid is squared-off when \[Theta] is small is due to the bounding box. This bothered me for a while, but I made a version where the line segment endpoints always formed a circle and found it a little too boring. The transition from squared-off to round adds visual interest that I think enhances the animation.
(Incidentally, to make alternate round version I ended up converting to ParametricPlot3D so that I could use RegionFunction, but it would have been nicer to be able to do it in Graphics3D. Is there any way to mimic the behavior of RegionFunction in a Graphics3D object?)