Some really simple parameterizations yield some elegant-looking results. Some of them are fractal. Here are a few of the coolest I found:
ParametricPlot[Sum[{1/(Sqrt[2])^k Sin[(Sqrt[2])^k t],1/(Sqrt[2])^k Cos[(Sqrt[2])^k t]}, {k, 0, 20}], {t, 0, 1200 Pi}]
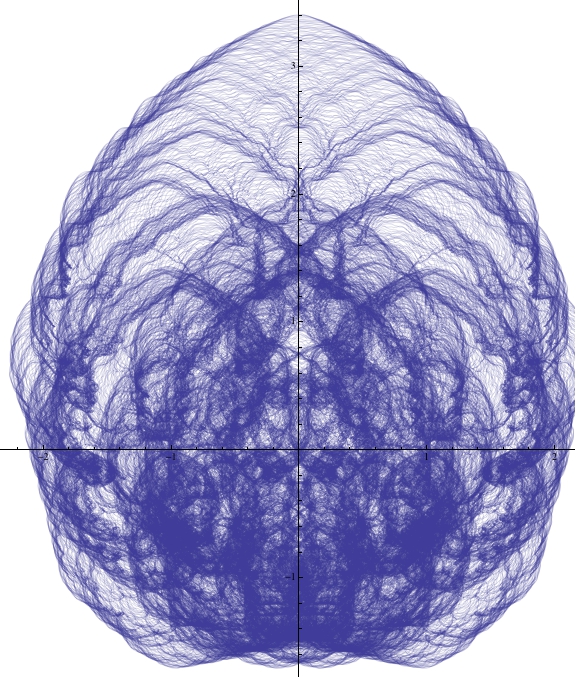
It almost looks photorealistic when we take t and k to large values, a bit like an electron microscope image.
ParametricPlot[Sum[{1/(Sqrt[3])^k Sin[(Sqrt[3])^k t],1/(Sqrt[3])^k Cos[(Sqrt[3])^k t]}, {k, 0, 20}], {t, 0, 1200 Pi}]
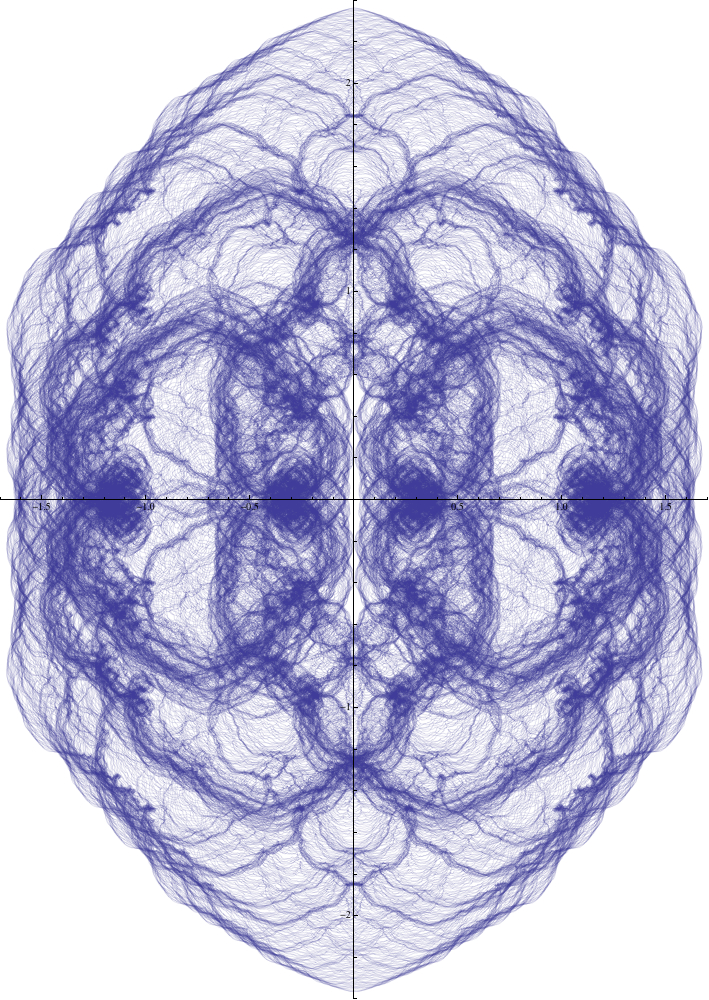
ParametricPlot[Sum[{1/GoldenRatio^k Sin[GoldenRatio^k t],1/GoldenRatio^k Cos[GoldenRatio^k t]}, {k, 0, 20}], {t, 0, 1200 Pi}]
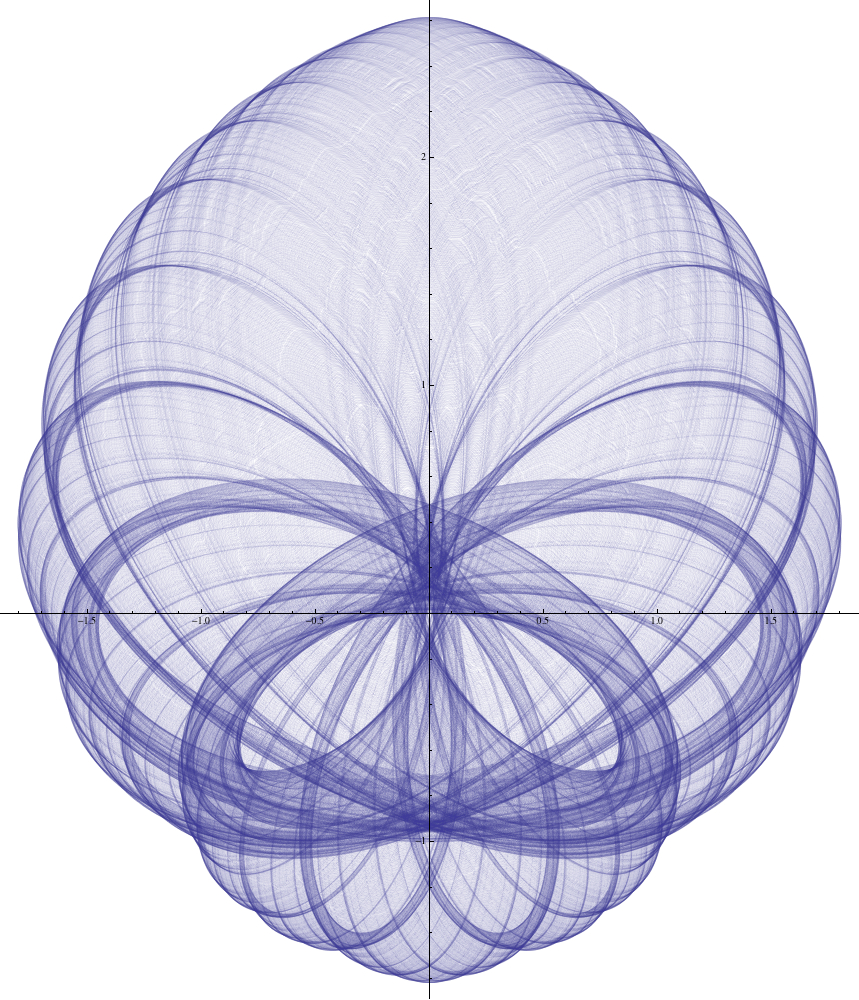
ParametricPlot[Sum[{1/Fibonacci[k] Sin[Fibonacci[k + 13] t],1/Fibonacci[k] Cos[Fibonacci[k + 13] t]}, {k, 1, 20}], {t, 0, 2 Pi}]
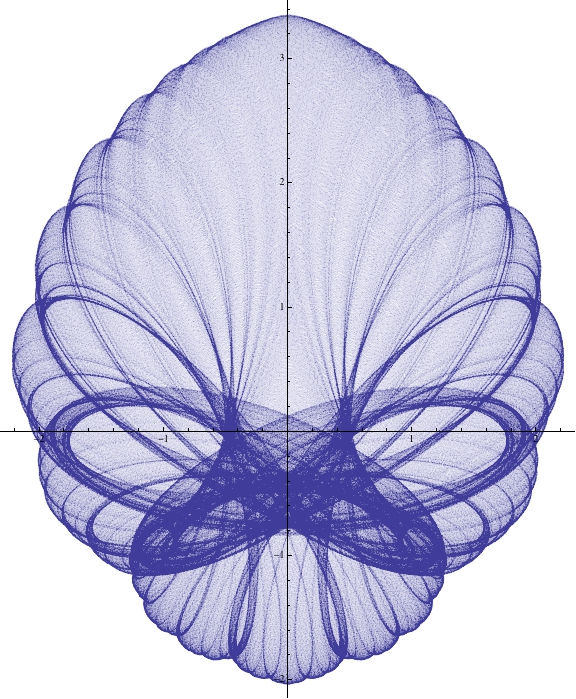
ParametricPlot[Sum[{(-1)^k/a^k Sin[a^k t], (-1)^k/a^k Cos[a^k t]}, {k, 0, 20}], {t, 0, 1200 Pi}]
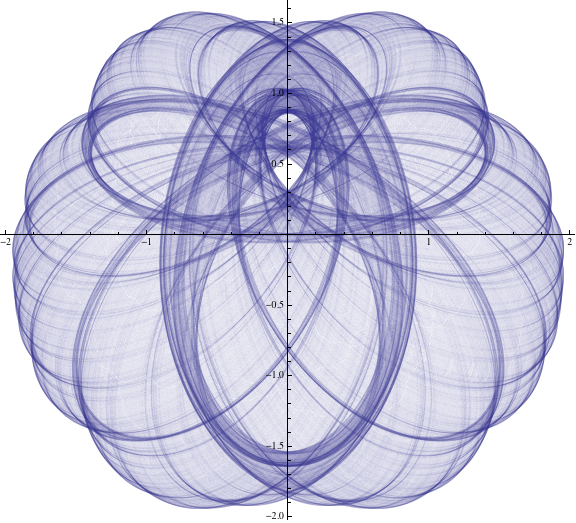
ParametricPlot[Sum[{1/k^2 Sin[k^2 t], 1/k^2 Cos[k^2 t]}, {k, 1, 100}], {t, 0, 2 Pi}]
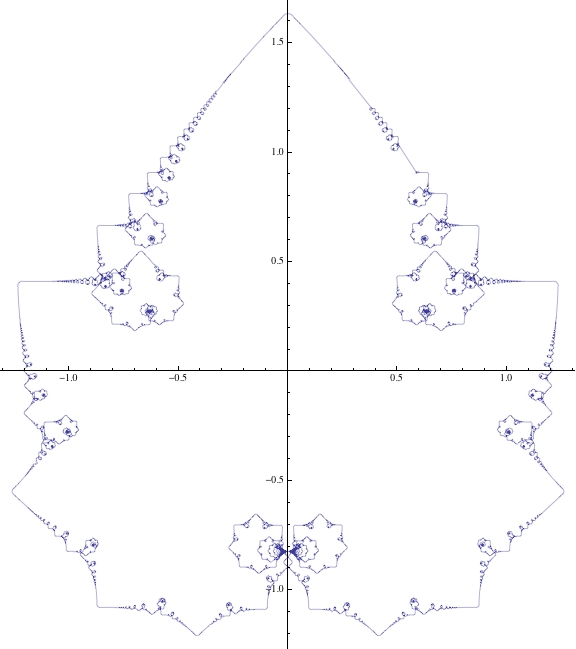
ParametricPlot[Sum[{1/2^k Sin[2^k t], 1/2^k Cos[2^k t]}, {k, 0, 50}], {t, 0, 2 Pi}]
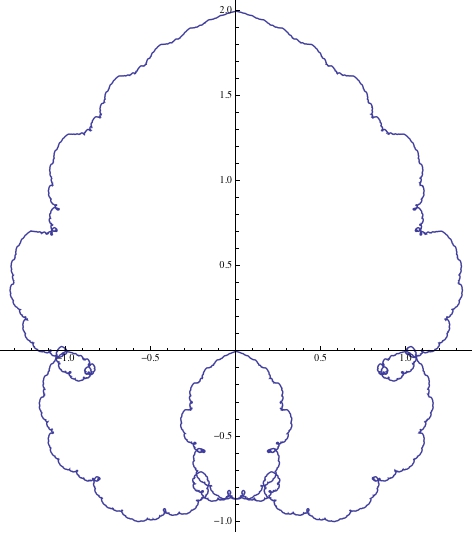
ParametricPlot[Sum[{1/Fibonacci[k] Sin[Fibonacci[k] t], 1/Fibonacci[k] Cos[Fibonacci[k] t]}, {k, 1, 30}], {t, 0, 2 Pi}]
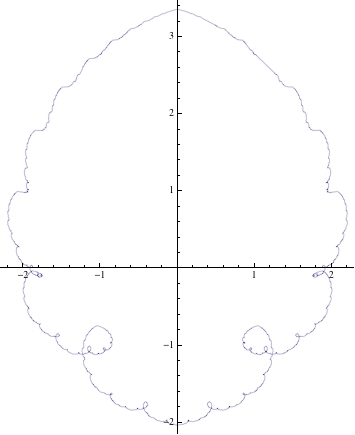
ParametricPlot[Sum[{(-1)^k/2^k Sin[2^k t], (-1)^k/2^k Cos[2^k t]}, {k, 0, 20}], {t, 0, 2 Pi}]
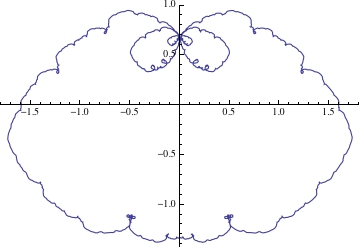
ParametricPlot[Sum[{1/Fibonacci[k] Sin[k^2 t], 1/Fibonacci[k] Cos[k^2 t]}, {k, 1, 150}], {t, 0, 2 Pi}]
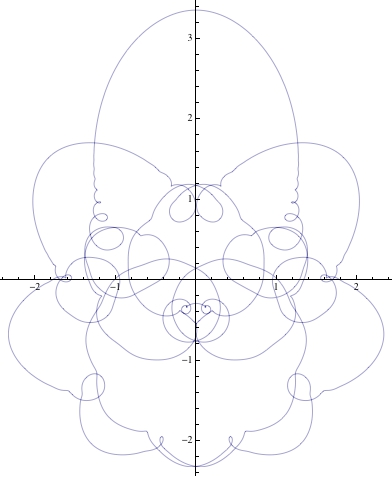
ParametricPlot[Sum[{(-1)^k/k! Sin[(-1)^k k! t], (-1)^k/k! Cos[(-1)^k k! t]}, {k, 0, 100}], {t, 0, 2 Pi}]
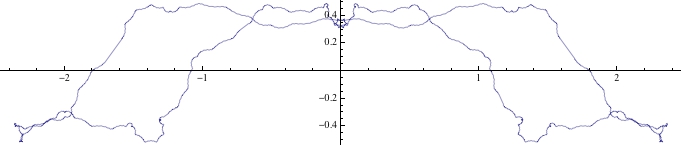
ParametricPlot[Sum[{(-1)^k/2^k Sin[(-1)^k 2^k t], (-1)^k/2^k Cos[(-1)^k 2^k t]}, {k, 0, 100}], {t, 0, 2 Pi}]
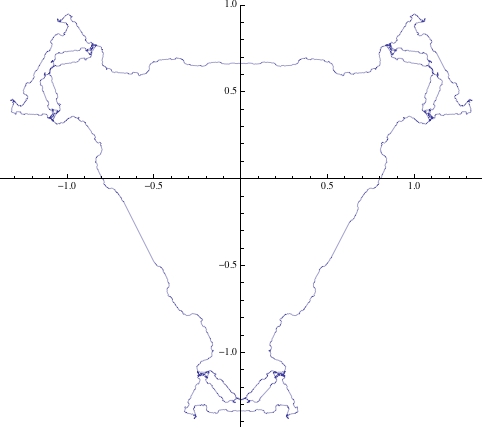
ParametricPlot[Sum[{(-1)^k/k^2 Sin[(-1)^k k^2 t], (-1)^k/k^2 Cos[(-1)^k k^2 t]}, {k, 1, 100}], {t, 0, 2 Pi}]
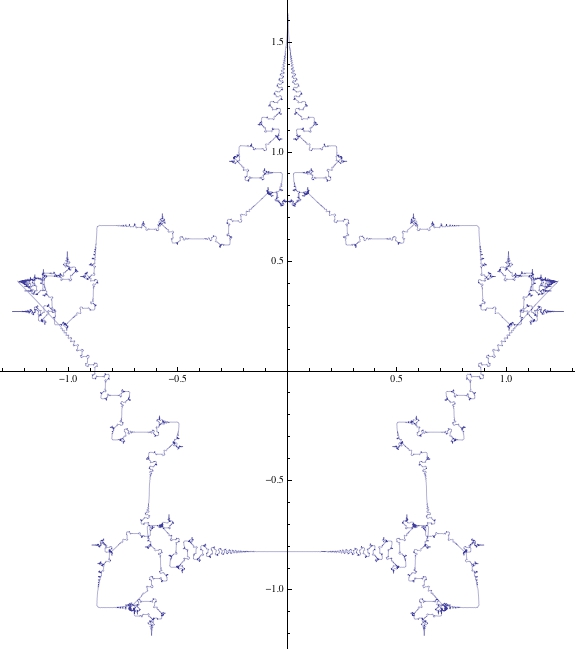
ParametricPlot[Sum[{(-1)^k/k^2 Sin[(-1)^k (k - 1)^2 t], (-1)^k/k^2 Cos[(-1)^k (k - 1)^2 t]}, {k, 1, 150}], {t, 0, 2 Pi}]
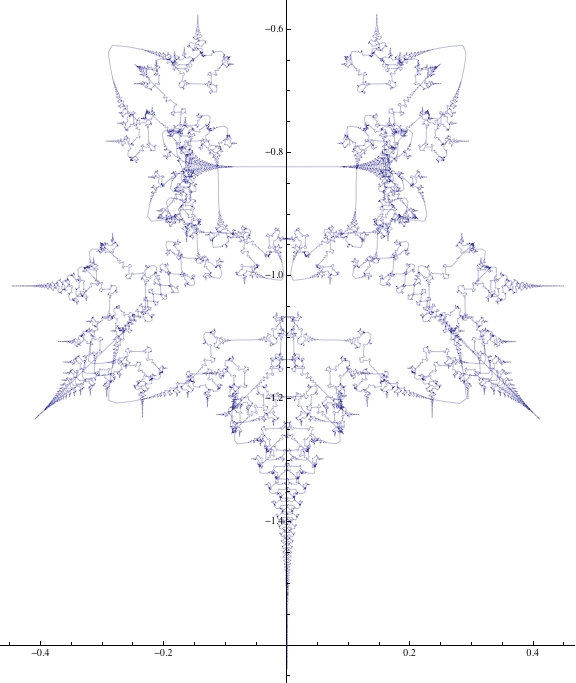
ParametricPlot[Sum[{1/k^2 Sin[(k - 1)^2 t], 1/k^2 Cos[(k - 1)^2 t]}, {k, 1, 150}], {t, 0, 2 Pi}]
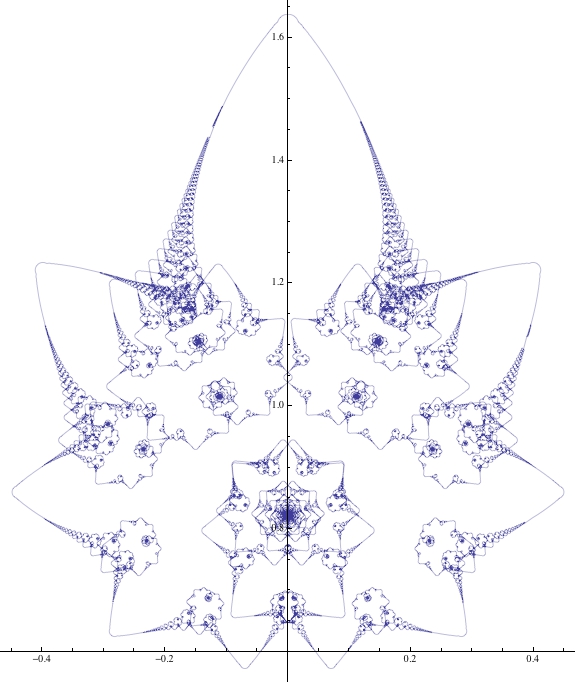
ParametricPlot[Sum[{1/Fibonacci[k] Sin[Fibonacci[k]^2 t], 1/Fibonacci[k] Cos[Fibonacci[k]^2 t]}, {k, 1, 30}], {t, 0, 2 Pi}]
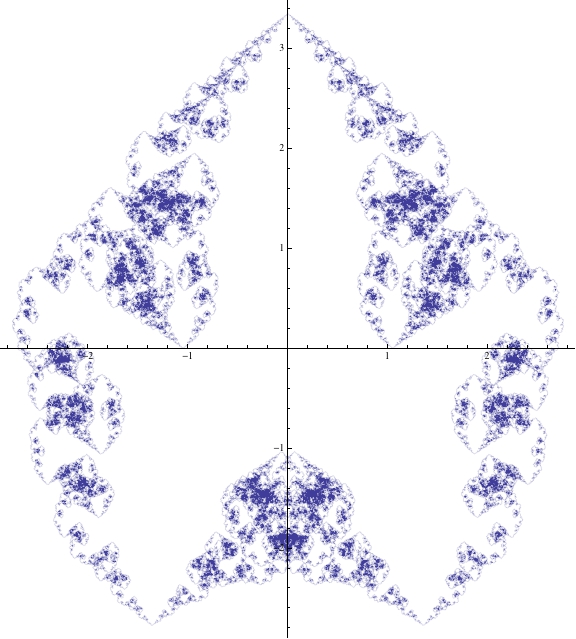
ParametricPlot[Sum[{1/Sqrt[Fibonacci[k]] Sin[Fibonacci[k] t],1/Sqrt[Fibonacci[k]] Cos[Fibonacci[k] t]}, {k, 1, 30}], {t, 0, 2 Pi}]
Please post any similar plots here!