I checked for round off error in the following and found some evidence of an error on Mathematica's part..
To keep expanding our list of identities,
Let m be the MRB constant:
m = NSum[(-1)^n (n^(1/n) - 1), {n, 1, Infinity},
Method -> "AlternatingSigns", WorkingPrecision -> 200]
(* 0.18785964246206712024851793405427323005590309490013878617200468408947\
7231564660213703296654433107496903842345856258019061231370094759226630\
438929348896184120837336626081613602738126379373435283224982*)
Then
m- Sum[(-1)^n (n^(1/n) - x/n)]==1/2 - Log[2^x]) for x up to and including x=20,
sl = Table[(m -
NSum[(-1)^n (n^(1/n) - x/n), {n, 1, Infinity},
Method -> "AlternatingSigns", WorkingPrecision -> 200]) - (
1/2 - Log[2^x]), {x, 2, 350}];Print[N[sl[[1 ;; 19]], 30],
N[sl[[340 ;; 349]], 30]]
(* {1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194,1.2429*10^-194
,0.0259183374259628836676682211919}
{2.26076864811449590986989210226*10^-14,-8.88315735092798090493028735628*10^-15,3.41440692151960990535420984521*10^-15,-1.28342528622733270311828562834*10^-15,4.71627690575458679289370587222*10^-16,-1.69380112008895556586806590448*10^-16,5.94313651116753436913326660086*10^-17,-2.03661686166157149664474358887*10^-17,6.81377121338534361189573743102*10^-18,-2.22478627625166599855471551340*10^-18,7.08668056816025010760503247866*10^-19}
*)
x=20 is the 18th element of sl. Notice that the 19th element is ,0.0259183374259628836676682211919.
But for x>20 something beautiful happens:
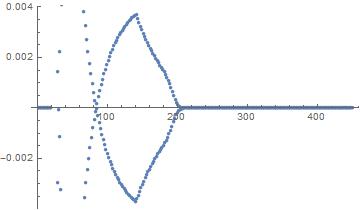
ListPlot[sl]
The reason for the poor behavior is that Sum[(-1)^n (n^(1/n) - x/n)] for x/n not equal to 1 is divergent. and as x gets large x/n is further from 1 and
NSum[(-1)^n (n^(1/n) - x/n), {n, 1, Infinity},
Method -> "AlternatingSigns", WorkingPrecision -> 200] /. x -> 10^t
for the most part goes to 10^(t - 1) Log[2^10] - 1/2 + m) as t gets large:
Table[NSum[(-1)^n (n^(1/n) - 10^t/n), {n, 1, Infinity},
Method -> "AlternatingSigns",
WorkingPrecision -> 200] - (10^(t - 1) Log[2^10] - 1/2 + m), {t,
10}]
(* {-1.3908983*10^-190, \
-0.0018047654004370285056973513785100572645865454457815534444526025649\
6588183515222563305775295474928095349258443231532776865726011389856029\
989033125798213015705226943409189152746974520337737698733944, \
-1.402096*10^-190, -1.50389*10^-190, -2.5218*10^-190, \
-1.2701*10^-189, -1.1450*10^-188, -1.1325*10^-187, -1.1312*10^-186, \
-1.1311*10^-185}*)
Notice that
NSum[(-1)^n (n^(1/n) - s^t/n), {n, 1, Infinity},
Method -> "AlternatingSigns",
WorkingPrecision ->
200]
for the most part goes to (s^(t - 1) Log[2^s] - 1/2 + m) Enter the following:
Table[N[NSum[(-1)^n (n^(1/n) - s^t/n), {n, 1, Infinity},
Method -> "AlternatingSigns",
WorkingPrecision -> 200] - (s^(t - 1) Log[2^s] - 1/2 + m),
10], {t, 10}, {s, 10}] // TableForm
In general we have,
NSum[(-1)^n (n^(1/n) - w/n), {n, 1, Infinity},
Method -> "AlternatingSigns", WorkingPrecision -> 200]
going to
( Log[2^w] - 1/2 + m). See next:
sll = Table[
NSum[(-1)^n (n^(1/n) - w/n), {n, 1, Infinity},
Method -> "AlternatingSigns",
WorkingPrecision -> 200] - (Log[2^w] - 1/2 + m), {w, 450}]; Print[
Print[N[sll[[1 ;; 20]], 30], N[sll[[340 ;; 349]], 30]]
(*{-1.3907965*10^-190,-1.3908079*10^-190,-1.3908192*10^-190,-1.3908305*10^-190,-1.3908418*10^-190,-1.3908531*10^-190,-1.3908644*10^-190,-1.3908757*10^-190,-1.3908870*10^-190,-1.3908983*10^-190,-1.3909097*10^-190,-1.3909210*10^-190,-1.3909323*10^-190,-1.3909436*10^-190,-1.3909549*10^-190,-1.3909662*10^-190,-1.3909775*10^-190,-1.3909888*10^-190,-1.3910001*10^-190,
-0.0259183374259628836676682211919}
{-1.394631*10^-190,-1.394642*10^-190,-1.394653*10^-190,-1.394665*10^-190,-1.394676*10^-190,-1.394687*10^-190,-1.394699*10^-190,-1.394710*10^-190,-1.394721*10^-190,-1.394733*10^-190}*)
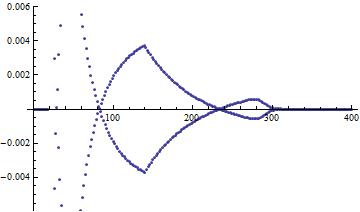
This is the same formula we started with, yet the results are a little different giving some evidence of an error on Mathematica's part.
ListPlot[sll]