Below are some results I got from Wolfram Alpha (W|A).
Viswanath's constant is one of those hard to calculate constants related to a random Random Fibonacci like Sequence. It is approximately 1.1319882487943.
The following snip is From Weisstein, Eric W. "Random Fibonacci Sequence." From MathWorld--A Wolfram Web Resource, http://mathworld.wolfram.com/RandomFibonacciSequence.html
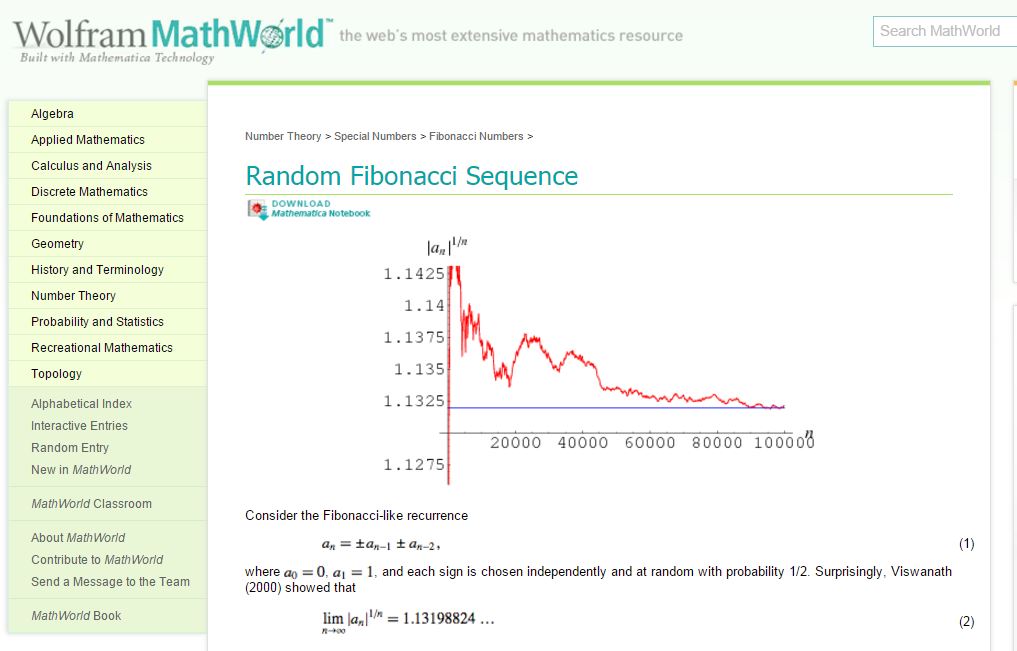
The bottom of that snip says,

I am interested in this Viswanath's constant, because it is the limit of some Fibonacci numbers to the power of 1/n. My fascination to formulas involving powers of 1/n comes from my original investigations into the MRB constant series,
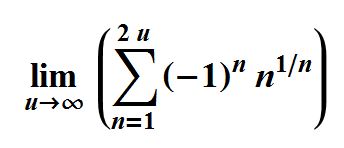
All my work at calculating MRB's digits is found at http://community.wolfram.com/groups/-/m/t/366628?ppauth=fiuT7kL7.
Here is how I arrived at the approximation:
In 2007 I noticed a one of many trivial formulas involving the MRB constant that produces numbers that have several repeating digits:
m = 0.187859642462067120248517934 (* Let m be an approximation MRB.*)
(1387/2500 - m)*Pi*30089
(*34685.9111111111249709407958*)
About an hour ago I went to W}A to see if it knew of my formula that gave the repeating number result of 34685.9111111111249709407958. W|A can find closed form approximations to many numbers! W\A didn't see the MRB approximation but it did see another one involving Viswanath's constant. It said:
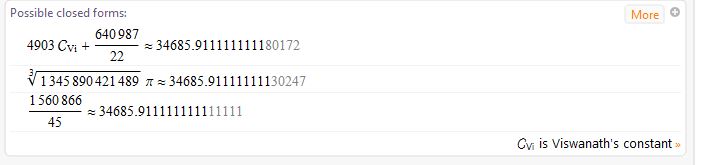
Using W\A's Viswanath formula I came up with an approximation to Viswanath from MRB:
Solve[4903 vv+640987/22==(1387/2500-m)*Pi*30089,vv]
(* {{vv -> 1.1319882487942887412224196}}*)
v = 1.1319882487943 (*Let v be a known approximation to Viswanath's constant.*)
v - 1.1319882487942887412224196 (*This gives the error of the MRB approximation to Viswanath:*)
(* 1.12921394143*10^-14*)
I know the chance is slim, but I am wondering if the MRB approximation is giving a truly useful approximation to Viswanath!
W\A also told me that the above error is found by an approximation using another constant, an Omega constant , giving this link for a definition;
https://en.wikipedia.org/wiki/Omega_constant . Here is what W|A said,
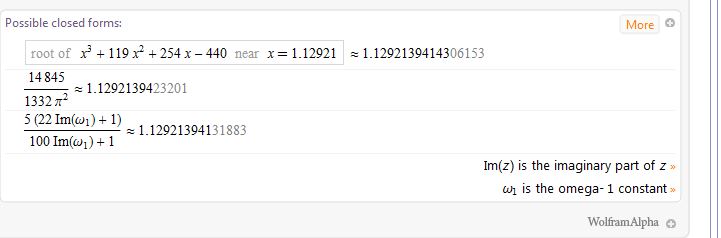
That last formula involving that omega constant might not be useful at all because Viswanath, v, could only be calculated to 13 decimal places and the error the omega formula was approximating of the order of 13 or 14 decimal places! If no one can find an algebraic connection involving powers of 1/n between MRB and Viswanath, we will have to wait until more Viswanath digits are known!