A force diagram (tension excluded) can be shown nicely for the grass example, as the dynamic forces are defined directly from equations of angular derivatives, and thus have already been calculated. This also helps stress how easy it is to play with said forces, as they are stuck in after all the hard work.
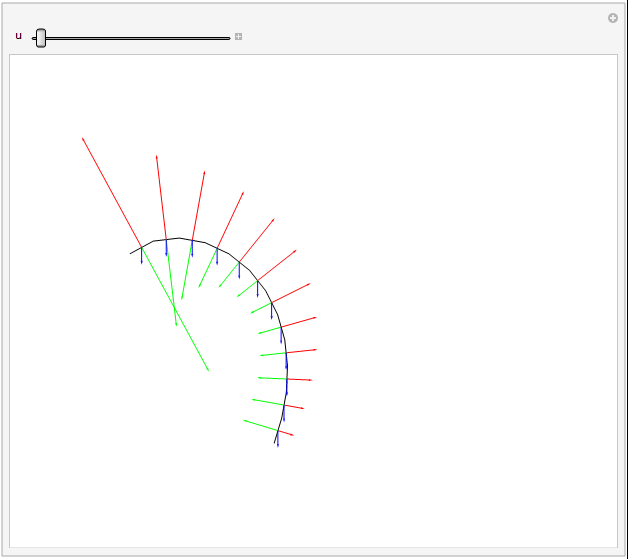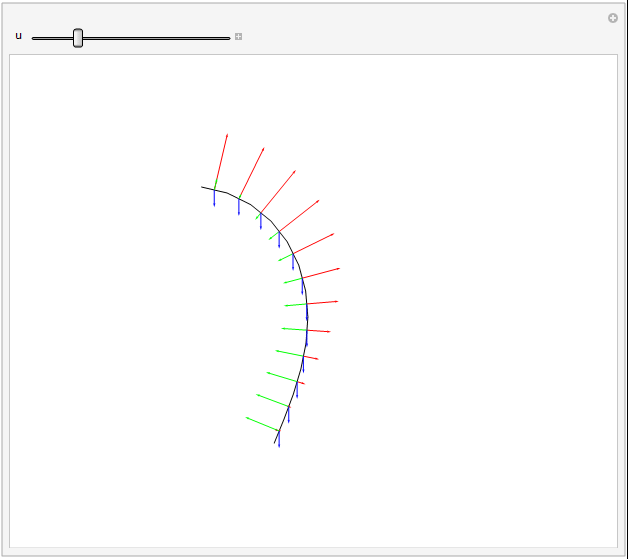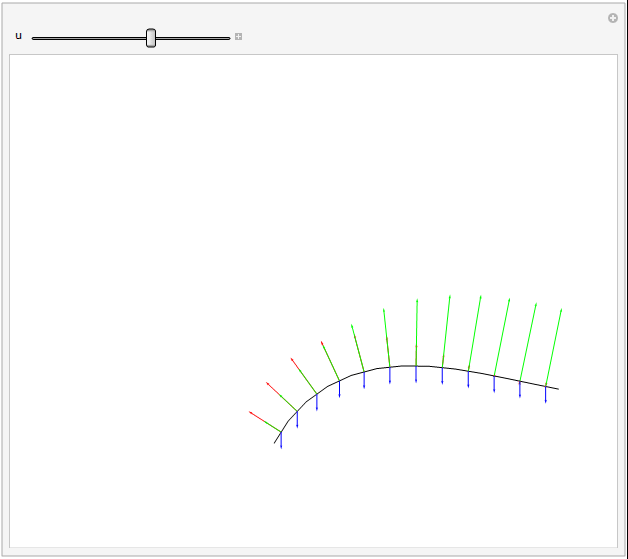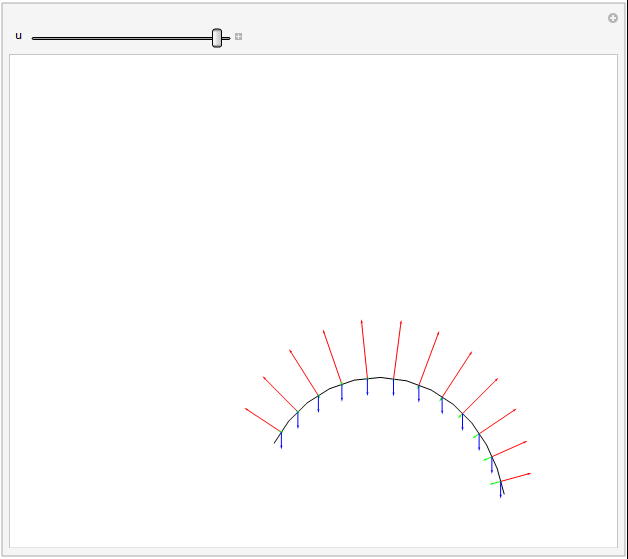
Arrows representing forces. Gravity, drag, and angular restorative forces are respectively blue, green, and red. Length proportional to square root of force magnitude.
The general equations would be as follows. All angle specified forces were appended, rather than worked with throughout (though you've incurred some self doubt here, I'll try to explicitly verify some assumptions soon.)
D[ MassOneX[t] ,{t,2}] = Sin[ AngleOne[t] ] TensionOne[t] + Sin[ AngleOne[t] ] TensionTwo[t]
D[ MassOneY[t] ,{t,2}] = Cos[ AngleOne[t] ] TensionOne[t] + Cos[ AngleOne[t] ] TensionTwo[t] + m g
...
D[ MassN-1X[t] ,{t,2}] = Sin[ AngleN-1[t] ] TensionN-1[t] + Sin[ AngleN-1[t] ] TensionN[t]
D[ MassN-1Y[t] ,{t,2}] = Cos[ AngleN-1[t] ] TensionN-1[t] + Cos[ AngleN-1[t] ] TensionN[t] + m g
D[ MassNX[t] ,{t,2}] = Sin[ AngleN[t] ] TensionN[t]
D[ MassNY[t] ,{t,2}] = Cos[ AngleN[t] ] TensionN[t] + m g