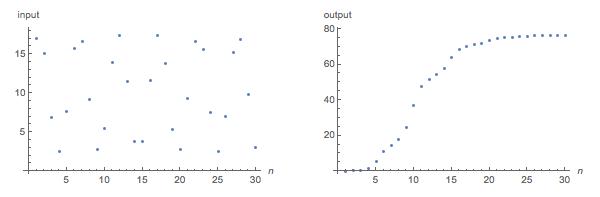
Given input-output sequences with uniform sampling of a natural growth process, I would like to estimate model parameters in a nonlinear difference equation. Here are example input-output sequences:
in = {16.969, 15.151, 6.83824, 2.51202, 7.62716, 15.7341, 16.6111, 9.15233, 2.76235, 5.4981, 13.9102, 17.392, 11.5535, 3.75623, 3.83153, 11.6845, 17.4135, 13.7951, 5.39155, 2.79867, 9.28573, 16.6734, 15.6468, 7.50031, 2.50563, 6.96037, 15.2477, 16.9184, 9.86588, 2.98251}
out = {0.1, 0.235755, 0.520125, 1.58736, 5.30637, 10.8286, 14.5398, 17.9214, 24.4315, 36.8878, 47.4856, 51.8436, 54.3319, 57.7956, 63.7485, 68.5763, 70.3306, 71.0822, 71.8903, 73.2932, 74.6665, 75.2082, 75.4013, 75.5603, 75.8267, 76.1532, 76.3087, 76.3591, 76.3908, 76.4382}
The model I would like to fit by estimating parameters a, b, & c and initial condition out[0]=out0 is
iter[a_, b_, c_, y0_] := Module[{}, Clear[y];
out[n_] :=
out[n] = out[n - 1] (1 + a*Exp[-(b in[[n - 1]] + c (n - 1))]);
out[0] := out0;
y /@ Range[Length[in]]];
FindFit would be ideal, as it allows setting initial parameter estimates, gradient method, as well as the norm function. However, I could not find any examples of FindFit using discrete time models such as this and I'm not sure of its applicability or required syntax.
I would appreciate any suggestions for a parameter estimation scheme suitable for this problem.