Write a list of 2012 numbers a[k] with a[k]=1/k on a white board

(1/Range[2012])//Short
{1,1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9,<<1999>>,1/2009,1/2010,1/2011,1/2012}

Erase any two numbers, $a$ and $b$, in the list and append $a + b + a \times b$ to the end of the list. Repeat this step for 2011 times.

Question: What is the number left?

• Example: Use a shorter list with 4 items

  example=1/Range[4] (*{1,1/2,1/3,1/4}*)
  

Step 1: Choose two numbers a, b

    RandomSample[example,2]
    (*{1,1/3}*)

Step 2: Remove a and b and append a+b+a*b

    l1={1/2,1/4,a+b+a*b}/.{a->1,b->1/3} (* {1/2,1/4,5/3}*)

Repeat step 1

    RandomSample[l1,2] (*{1/2,1/4}*)

Repeat step 2

    l2 = {5/3, a + b + a*b} /. {a -> 1/2, b -> 1/4} (* {1/2,1/4,5/3}*)

Now we only have two numbers left. Compute a+b+a*b yields

      a + b + a*b /. {a -> 5/3, b -> 7/8} (* result is 4*)

Let's try some code to solve it!

Brutal Force is never a bad choice on small sample size

pad[{a_, b_}] = a + b + a*b;
runTest[n_] := Module[{res = 1/Range[n], old, erase, , temp, grid},
  old = {};
  While[Length[res] >= 2,
   erase = 
    RandomSample[Range[Length[res]], 
     2];(*choose two unique numbers to be removed*)
   old = res;
   res[[erase]] = {Missing[], 
     Missing[]};(*make the chosen number missing!*)

   res = Append[DeleteMissing[res], pad[old[[erase]]]];
   Print["Remove: ", old[[erase]], " Add: ", pad[old[[erase]]], 
    " New list: ", res]
   ];
  Framed[Row@{"Result is ", res[[1]]}]
  ]

You can run the code above you will find the that runTest[n] always yields n. Therefore the solution to the problem here is $\boxed{2012}$.

Use the strong symbolic nature of Wolfram language to prove this result

Well lets take a look at this problem from a very mechanical way. Assume we have two numbers only:

pad[{a,b}]
a+b+a b

For list with 3 items, any choice of the two items to be removed will yield the same thing:

threeItems=pad[{c,pad[{a,b}]}]//Expand
==>a+b+a b+c+a c+b c+a b c

pad[{b,pad[{a,c}]}]//Expand
==>a+b+a b+c+a c+b c+a b c

pad[{a,pad[{b,c}]}]//Expand
==>a+b+a b+c+a c+b c+a b c

Hard to see the pattern here?

Take look at the result closely:

Cases[threeItems,p_/;Length[p]==#]&/@{0,2,3}(*items in the sum*)
==> {{a,b,c},{a b,a c,b c},{a b c}}

Use this Case function to all expanded expression above yields the same list we just obtained. The pattern of the list above is called rotational symmetry, meaning the order of the three items does not affect the result of the sum. Lets add a fourth item here:

pad[{d,pad[{a,pad[{b,c}]}]}]//Expand
===> a+b+a b+c+a c+b c+a b c+d+a d+b d+a b d+c d+a c d+b c d+a b c d

Separate the terms by its exponential/order from the the sum .The terms below also shows its invariance regarding to the permutation of the tuple {a,b,c,d}.

fourItems=Cases[%,p_/;Length[p]==#]&/@{0,2,3,4}
==> {{a,b,c,d},{a b,a c,b c,a d,b d,c d},{a b c,a b d,a c d,b c d},{a b c d}}

Now lets carefully count the number of items in each list above and prepend 1 to this list:

{1}~Join~(Length/@%)
{1,4,6,4,1}

Lets try again with the list {a,b,c,d,e} with 5 items

pad[{e,pad[{d,pad[{a,pad[{b,c}]}]}]}]//Expand
a+b+a b+c+a c+b c+a b c+d+a d+b d+a b d+c d+a c d+b c d+a b c d+e+a e+b e+a b e+c e+a c e+b c e+a b c e+d e+a d e+b d e+a b d e+c d e+a c d e+b c d e+a b c d e

Again, we group the items by their order and extract the length of each group:

fiveItems=Cases[%,p_/;Length[p]==#]&/@{0,2,3,4,5}
{{a,b,c,d,e},{a b,a c,b c,a d,b d,c d,a e,b e,c e,d e},{a b c,a b d,a c d,b c d,a b e,a c e,b c e,a d e,b d e,c d e},{a b c d,a b c e,a b d e,a c d e,b c d e},{a b c d e}}

{1}~Join~(Length/@fiveItems)
==> {1,5,10,10,5,1}

If you are familiar with Pascal's triangle or the binomial triangle, you should know immediately how to generate the sums we have shown so far:

var=x+{a,b,c,d}
==> {a+x,b+x,c+x,d+x}

Times@@var
==> (a+x) (b+x) (c+x) (d+x)

res1=%//Expand
==> a b c d+a b c x+a b d x+a c d x+b c d x+a b x^2+a c x^2+b c x^2+a d x^2+b d x^2+c d x^2+a x^3+b x^3+c x^3+d x^3+x^4  

The sum that we are looking for is

 res1/.x->1
 ==> 1+a+b+a b+c+a c+b c+a b c+d+a d+b d+a b d+c d+a c d+b c d+a b c d

given that the list contains 4 items. We can use the following functions to count the number of coefficient with pattern match (CountItem[ele_] is an enhanced version of this function ):

coefList=Coefficient[res1,x,#]&/@Range[0,Length[var]]
==> {a b c d,a b c+a b d+a c d+b c d,a b+a c+b c+a d+b d+c d,a+b+c+d,1}

countItem[ele_]:=Switch[ele,_Times, 1 ,_Plus,Length[List@@ele],_,1]

countItem/@coefList
==> {1,4,6,4,1}

Therefore, we know that we can calculate the result simply with the this expression:

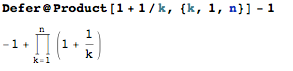
We don't have to expand the product to compute the result. For example, given a list of 10 items, each factor is simply:

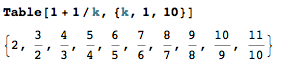
The denominator of one item cancels the numerator of the predecessor. Thus the result of the given product is $11$, aka the numerator of the last item. Do not forget to subtract 1 from the product to calculate the sum in the problem.