Here's how I would go about it,
solns =
Solve[((1 - b)^2) (R - r)^2 == 2 r*(1 + b)^2, r][[All, 1, 2]]
(* {(
1 + 2 b + b^2 + R - 2 b R + b^2 R - Sqrt[
1 + 4 b + 6 b^2 + 4 b^3 + b^4 + 2 R - 4 b^2 R + 2 b^4 R])/(
1 - 2 b + b^2), (
1 + 2 b + b^2 + R - 2 b R + b^2 R + Sqrt[
1 + 4 b + 6 b^2 + 4 b^3 + b^4 + 2 R - 4 b^2 R + 2 b^4 R])/(
1 - 2 b + b^2)} *)
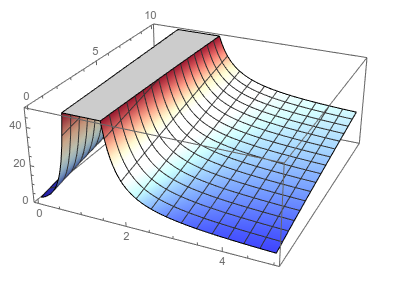
You have to be careful as there is a singularity in the second solution when b=1:
Limit[#, b -> 1] & /@ solns
(* {0, ?} *)
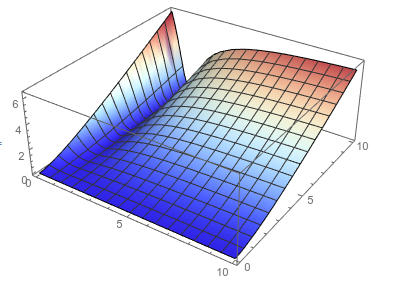
So you can plot the first solution over any range,
Plot3D[solns[[1]], {b, 0, 10}, {R, 0, 10}, PlotRange -> All,
ColorFunction -> "ThermometerColors"]
But the second solution you are limited in the range
Plot3D[solns[[2]], {b, 0, 5}, {R, 0, 10}, PlotPoints -> 100,
PlotRange -> {0, 50}, ColorFunction -> "ThermometerColors"]