Here's how I would go about it,

solns = 
 Solve[((1 - b)^2) (R - r)^2 == 2 r*(1 + b)^2, r][[All, 1, 2]]
(* {(
 1 + 2 b + b^2 + R - 2 b R + b^2 R - Sqrt[
  1 + 4 b + 6 b^2 + 4 b^3 + b^4 + 2 R - 4 b^2 R + 2 b^4 R])/(
 1 - 2 b + b^2), (
 1 + 2 b + b^2 + R - 2 b R + b^2 R + Sqrt[
  1 + 4 b + 6 b^2 + 4 b^3 + b^4 + 2 R - 4 b^2 R + 2 b^4 R])/(
 1 - 2 b + b^2)} *)

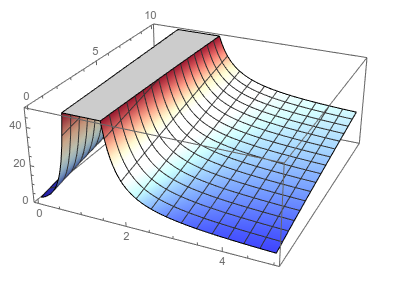
You have to be careful as there is a singularity in the second solution when b=1:

Limit[#, b -> 1] & /@ solns
(* {0, ?} *)

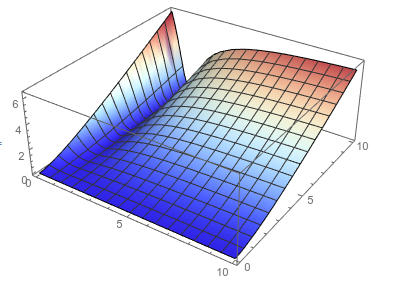
So you can plot the first solution over any range,

Plot3D[solns[[1]], {b, 0, 10}, {R, 0, 10}, PlotRange -> All, 
 ColorFunction -> "ThermometerColors"]

But the second solution you are limited in the range

Plot3D[solns[[2]], {b, 0, 5}, {R, 0, 10}, PlotPoints -> 100, 
 PlotRange -> {0, 50}, ColorFunction -> "ThermometerColors"]

In my post above, I put the output in comment markers - that is, anything between the (* and the *) are commented out.

So when you type the Solve command (note that you use two equal signs and not one, look at the help for Solve to see examples),

Solve[((1 - b)^2)/r^2 == 2*((1 + b)^2)/(R - r)^2, r]

this is the output,

{{r -> (-R + 2 b R - b^2 R - 
    Sqrt[2] Sqrt[R^2 - 2 b^2 R^2 + b^4 R^2])/(
   1 + 6 b + b^2)}, {r -> (-R + 2 b R - b^2 R + 
    Sqrt[2] Sqrt[R^2 - 2 b^2 R^2 + b^4 R^2])/(1 + 6 b + b^2)}}

This is in the form of a replacement rule ( type r^2 /. r->7 to see how a replacement rule works). But I wanted to grab the actual answers without copying and pasting them.

Here is another way to visualize your function:

define a function to be the solutions to the equations,

func[b_, R_] = 
  r /. Solve[((1 - b)^2)/r^2 == 2*((1 + b)^2)/(R - r)^2, r];
Plot[func[b, 1.0], {b, 0, 5}, Evaluated -> True]

These are the solutions for the equation when R=1.0, and you can plot them for any value of R.

I see. Very nice. I have also played with the syntax and gotten a feel for the function I am plotting.

I appreciate the help. Thanks. I have a lot to learn about the minutia in using Mathematica.