Under Scrutiny
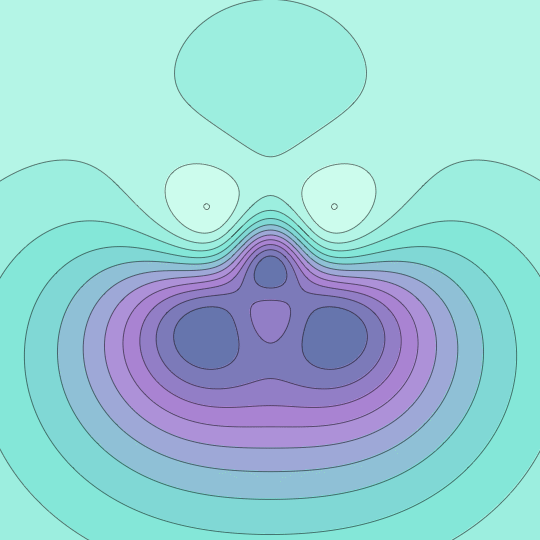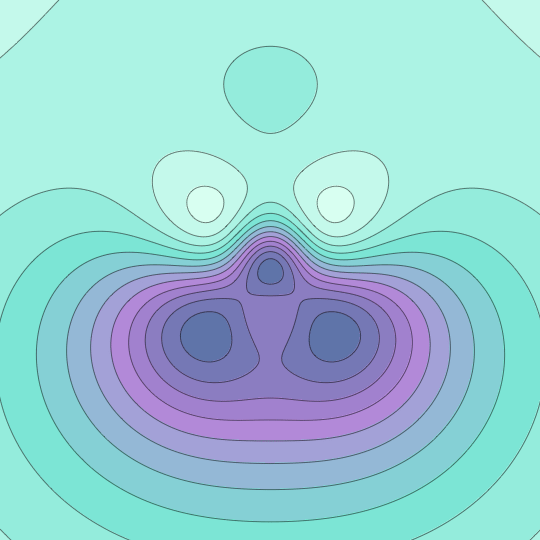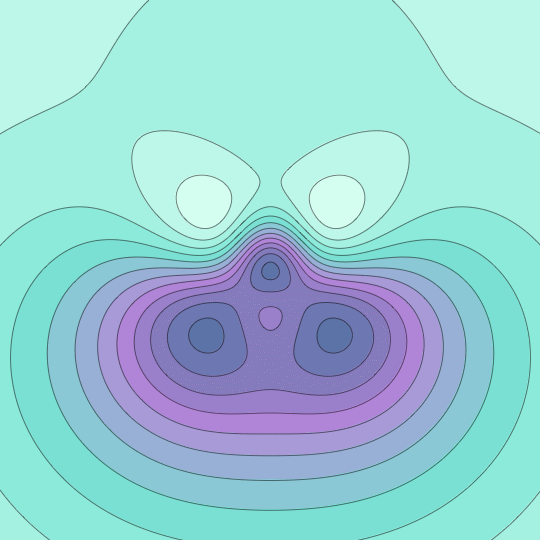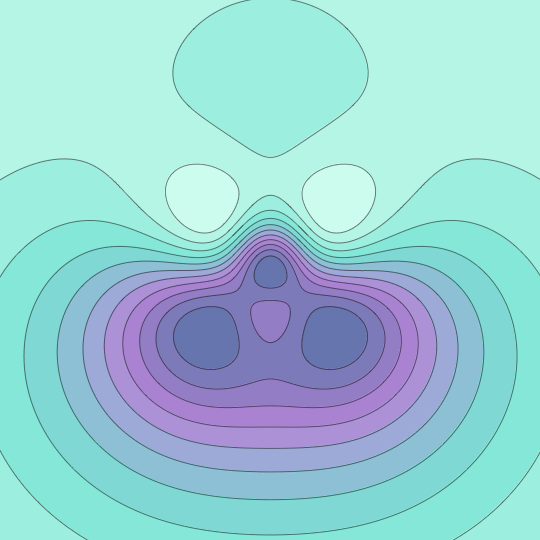
The last GIF got me thinking about Morse functions. This GIF shows the stereographic image of the level sets of the function $f(x,y,z)=x^3 + y^3 + z^3$ on the unit sphere.
Here's the code (add more points if you want to export nice images; I used PlotPoints->100 to produce the GIF):
InverseStereo[{x_, y_}] := 1/(1 + x^2 + y^2) {2 x, 2 y, x^2 + y^2 - 1};
Manipulate[
ContourPlot[#[[1]]^3 + #[[2]]^3 + #[[3]]^3 &[
InverseStereo[RotationMatrix[-Pi/4].{x, y}]], {x, -3,
3}, {y, -3, 3}, Axes -> None, ImageSize -> 540, Frame -> False,
PlotRangePadding -> -0.01,
Contours -> Table[r + t, {r, -7/6, 1, 1/6}],
ColorFunction -> (Blend[
RGBColor /@ {"#5B73A7", "#B485D8", "#78E4D4",
"#D8FFF1"}, #] &)], {t, 1/6, 0}]