You might be familiar with the Fano plane. One way to obtain it is to select triples from 1 to 7 that have a binary bit sum of 0. It's an example of a projective plane.

Projective plane rules

1. Every point pair defines a line.
2. Every line pair defines a point.
3. There are 4 points not on a line.

Code:

Select[Subsets[Range[7], {3}], BitXor @@ # == 0 &]

These can be arranged so that each triplet (123 145 167 246 257 347 356) is on an arc or a line.

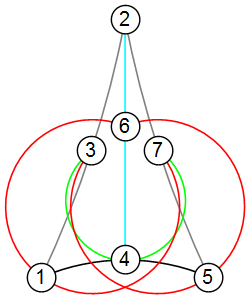
So how to draw a bunch of nice arcs and lines? Here's some code I whipped up.

ArcDraw2D[{threepoints_}] := 
  Module[{colinearitytest, circle, center, radius, angles, ends},
   colinearitytest = Chop[N[Det[Append[#, 1] & /@ threepoints]]];
   If[colinearitytest != 0,
    circle = Circumsphere[threepoints];
    center = N[circle[[1]]];  radius = N[circle[[2]]];
    angles = Mod[N[Arg[(# - center).{1, I}]/Pi], 2] & /@ threepoints;
    ends = {angles[[1]], angles[[3]]};
    If[angles == Sort[angles] || angles == Reverse[Sort[angles]],
     Circle[center, radius, Pi ends],
     Circle[center, radius, Pi {Max[ends], 2 + Min[ends]}]],
    Line[threepoints]]];

Now, let's extend that. Select[Subsets[Range[15], {3}], BitXor @@ # == 0 &] gives the next step up: triples from 1-15 with a BitXor sum of 0. I'll rearrange the output a bit.

pg23 = {{1, 4, 5}, {8, 9, 1}, {2, 10, 8}, {14, 12, 2}, {5, 11, 14},
   {1, 3, 2}, {2, 7, 5}, {5, 13, 8}, {8, 6, 14}, {14, 15, 1},
   {2, 6, 4}, {14, 7, 9}, {5, 15, 10}, {1, 13, 12}, {8, 3, 11},
   {6, 11, 13}, {7, 4, 3}, {15, 9, 6}, {13, 10, 7}, {3, 12, 15},
   {15, 8, 7}, {13, 2, 15}, {3, 14, 13}, {6, 5, 3}, {7, 1, 6},
   {9, 3, 10}, {10, 6, 12}, {12, 7, 11}, {11, 15, 4}, {4, 13, 9},
   {9, 2, 11}, {10, 14, 4}, {12, 5, 9}, {11, 1, 10}, {4, 8, 12}};

Now a bit of set-up for the graphic.

numbers = {8, 2, 14, 5, 1,   3, 6, 7, 15, 13,    11, 4, 9, 10, 12};
locations = Flatten[MapIndexed[
    RootReduce[{Sin[2 (#2[[2]] - 2) Pi/5], 
        Cos[2 (#2[[2]] - 2) Pi/5]} {2, .5, -1.378}[[#2[[1]]]]] &, 
    Partition[numbers, 5], {2}], 1];
newloc = Last /@ Sort[Transpose[{numbers, locations}]];
colors = {Black, Gray, Cyan, Green, Red, Yellow, Blue}; 

Then we can go right to the graphic.

Graphics[{AbsoluteThickness[1.6],
  MapIndexed[{colors[[Ceiling[#2[[1]]/5]]], ArcDraw2D[newloc[[#1]]]} &, pg23],
  MapIndexed[{{Black, Disk[#1, .12]}, {White, Disk[#1, .11]},
     Style[Text[#2[[1]], #1], 20]} &, newloc]}, 
 ImageSize -> {500, 500}]

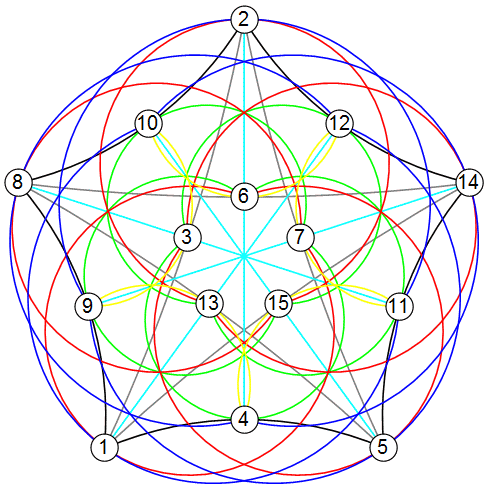
If you look close, you can see the Fano plane from the opener in here. There are 15 Fano planes of 3 different types. To see these in 3D, take a look at 15 Point Projective Space.

An alternative geometry allows lines that don't intersect, otherwise known as parallel lines.

Affine plane rules

1. Every point pair defines a line.
2. Every point-line pair defines a line.
3. There are 4 points that define 6 lines.

One affine plane example is the Game of Set, where each of 81 card has three possibilities for the attributes number, color, shape, and shading. In a line of three Set cards, the values for a given attribute will be either all the same or all different. There are 1080 ways to get a Set triplet.

Select[Subsets[Range[1, 81], {3}], Total[Mod[Total[IntegerDigits[#, 3, 4]], 3]] == 0 &]

Is there another nice affine plane where all lines have 3 points? Yes, within elliptic curves. Take triplets from the integers that add to zero. Now place them on the plane so that all triplets are on a straight line. You might get an image like the following:

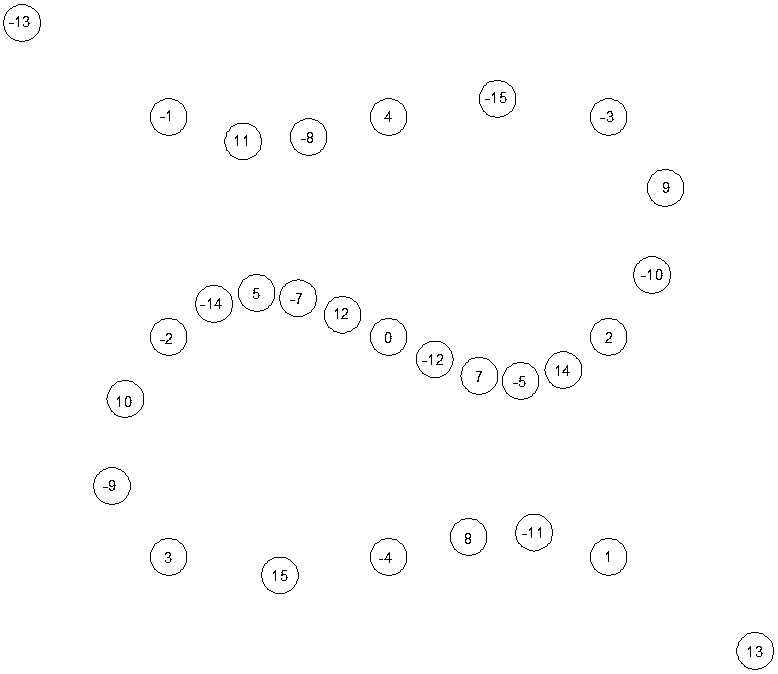
If you pick any triplet with a sum of 0, you'll find it is on a straight line. To add new numbers, pick two pairs with the opposing sum, such as {1-,-15} and {-2,-14} for 16. The new number will go to the intersection point of the two lines.