Group Abstract Group Abstract

Message Boards Message Boards

0
|
3.8K Views
|
2 Replies
|
2 Total Likes
View groups...
Share
Share this post:

Usage of MeshRefinementFunction

I've trying to use MeshRefineFunction, but found unusual behavior:

When I define a simple function like so:

ClearAll[meshRefine]
meshRefine[vertices_, area_] := area > 0.0001
mesh = Polygon[{{1, 0}, {0, 1.8}, {-1, 0}}];
DiscretizeRegion[mesh, MeshRefinementFunction -> meshRefine]

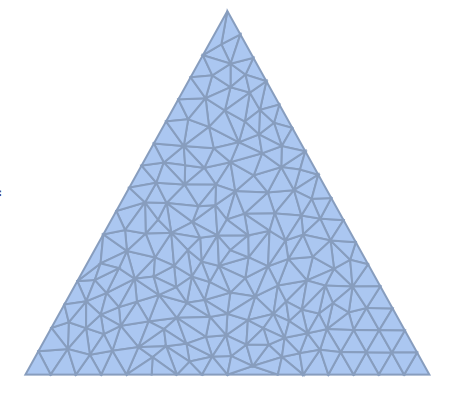
enter image description here

The output seems to be independent of the number that I put after area.

It does work if I make the following construct:

  ClearAll[meshRefine]
  meshRefine = Function[{vertices, area},
     Module[{mean},
      (*mean=Mean[vertices];
      mean=Norm[mean];*)

      area > 0.001
      ]
     ];
  mesh = Polygon[{{1, 0}, {0, 1.8}, {-1, 0}}];
  DiscretizeRegion[mesh, MeshRefinementFunction -> meshRefine]

enter image description here

but does not if I do the following:

ClearAll[meshRefine]
meshRefine = Function[{vertices, area},
   Module[{mean},
    mean=Mean[vertices];
    mean=Norm[mean];

    area > 0.001
    ]
   ];
mesh = Polygon[{{1, 0}, {0, 1.8}, {-1, 0}}];
DiscretizeRegion[mesh, MeshRefinementFunction -> meshRefine]

and note that I do not use the variable mean whatsoever!

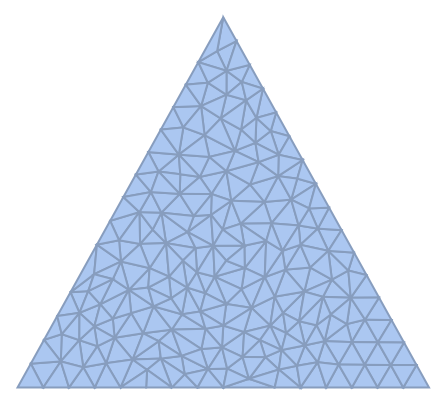
enter image description here

can someone explain me this behavior?

(Mathematica 10.4 on El Capitan)
POSTED BY: Sander Huisman
2 Replies
Sort By:

I guess it would've been something related to compile, but the function does get evaluated at many points, see example below, so that made me second-guess... Is there a way around it? (slow is OK) I would like to call a nearestfunction generated by nearest (or a regiondistancefunction) (basically refine it more around some points). Basically writing a nearest function myself is possible of course...

ClearAll[meshRefine]
\[CurlyPhi] = 0;
p = {};
Dynamic[\[CurlyPhi]]
meshRefine[vertices_, area_] := (\[CurlyPhi]++; 
  AppendTo[p, Mean[vertices]]; area > 0.00001)
mesh = Polygon[{{1, 0}, {0, 2.2}, {-1, 0}}];
DiscretizeRegion[mesh, MeshRefinementFunction -> meshRefine]
p // Point // Graphics

Yeah, indeed a warning would've been nice ;) well, I guess I have to refine it manually after it somehow... that's unfortunate....

Thank Ilian for the feedback!
POSTED BY: Sander Huisman

The basic problem is that the mesh refinement function needs to be compiled (because it is being used as a LibraryLink callback function). When something goes wrong with this automatic compilation, the discretization will proceed but the refinement function will be ignored.

I realize this is not made clear by the documentation, and in any case, there should be at least a warning message. Thank you for bringing this to our attention.

For the first example, try

ClearAll[meshRefine]
meshRefine[vertices_, area_] := area > 0.001
mesh = Polygon[{{1, 0}, {0, 1.8}, {-1, 0}}];
DiscretizeRegion[mesh, MeshRefinementFunction -> Function[{v, a}, Evaluate[meshRefine[v, a]]]]

For the last example, the compiler has trouble figuring out whether your mean is a rank-1 tensor or a scalar. Try

ClearAll[meshRefine]
meshRefine = 
  Function[{vertices, area}, 
   Module[{meanv, meann}, meanv = Mean[vertices];
    meann = Norm[meanv];
    area > 0.001]];
mesh = Polygon[{{1, 0}, {0, 1.8}, {-1, 0}}];
DiscretizeRegion[mesh, MeshRefinementFunction -> meshRefine]
POSTED BY: Ilian Gachevski
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard