Dear Hans,

you are quite right. I should have given your solution first. I was thinking about problems with more points.

coords = RandomReal[1, {3000, 3}];
AbsoluteTiming[Outer[EuclideanDistance, coords, coords, 1];]

evaluates in 7.17301 seconds on my MacBook, whereas

AbsoluteTiming[Table[Norm[coords[[i]] - coords[[j]]], {i, 3000}, {j, 3000}];]

evaluates in 50.5653 seconds. Here is a graphic to illustrate the comparison.

Monitor[result = 
  Reap[For[m = 0, m <= 2500, coords = RandomReal[1, {m, 3}]; 
     Sow[{m, First[
        AbsoluteTiming[Outer[EuclideanDistance, coords, coords, 1];]],
        First[AbsoluteTiming[
         Table[Norm[coords[[i]] - coords[[j]]], {i, 1, m}, {j, 1, 
            m}];]]}]; m = m + 100]][[2, 1]], m]

and then

ListLinePlot[{Legended[result[[All, {1, 2}]], "functional"], Legended[result[[All, {1, 3}]], "procedural"]}, LabelStyle -> Directive[Bold, Medium]]

which gives

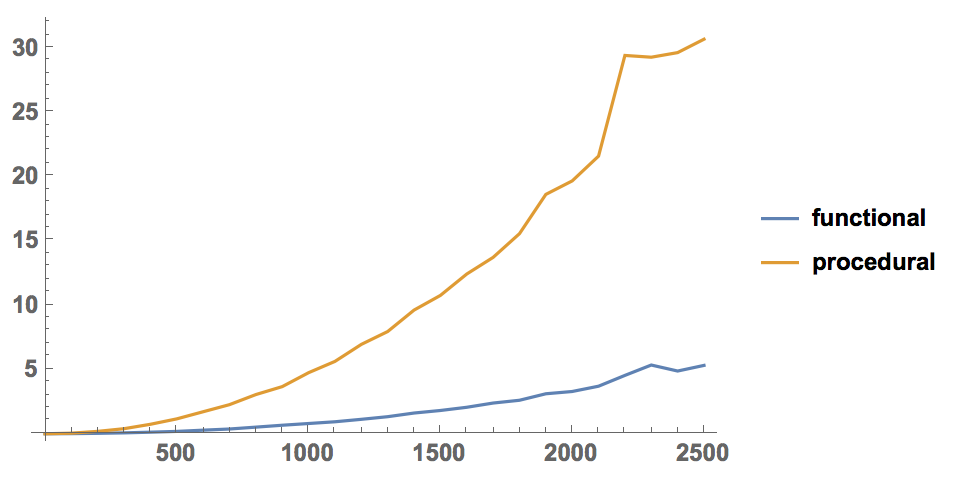
Of course, the difference for small numbers of points is inconsequential.

Cheers,

Marco