Hi Ed,
if you use "Mesh-> All" you see that this is a plotting issue:
eqnsDiff[\[Alpha]_, \[Beta]_, \[Epsilon]_, \[Delta]_, \[Mu]_, x0_,
y0_] := {x'[t] ==
x[t] (1 -
x[t]) - (\[Alpha] x[t] y[t])/(1 + \[Beta] x[t] + \[Mu] y[t]),
y'[t] == \[Epsilon] (x[t] y[
t])/(1 + \[Beta] x[t] + \[Mu] y[t]) - \[Delta] y[t],
x[0] == x0, y[0] == y0}
tf = 500;
tsamp = 2;
npoints = Ceiling[(tf/tsamp) + 1];
s1 = NDSolve[
eqnsDiff[1, 13/10, 4, 4/10, 1/10000, 15/100, 5/10], {x, y}, {t, 0,
tf}];
Plot[Evaluate[{x[t], y[t]} /. s1], {t, 0, tf}, ImageSize -> Large,
Mesh -> All]
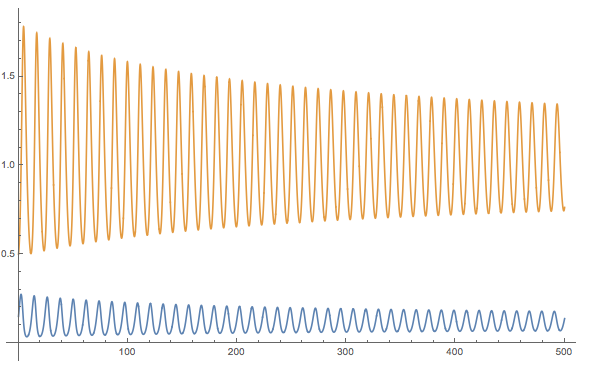
This is a bit unexpected but only shows that you just need to plot some more points:
eqnsDiff[\[Alpha]_, \[Beta]_, \[Epsilon]_, \[Delta]_, \[Mu]_, x0_,
y0_] := {x'[t] ==
x[t] (1 -
x[t]) - (\[Alpha] x[t] y[t])/(1 + \[Beta] x[t] + \[Mu] y[t]),
y'[t] == \[Epsilon] (x[t] y[
t])/(1 + \[Beta] x[t] + \[Mu] y[t]) - \[Delta] y[t],
x[0] == x0, y[0] == y0}
tf = 500;
tsamp = 2;
npoints = Ceiling[(tf/tsamp) + 1];
s1 = NDSolve[
eqnsDiff[1, 13/10, 4, 4/10, 1/10000, 15/100, 5/10], {x, y}, {t, 0,
tf}];
Plot[Evaluate[{x[t], y[t]} /. s1], {t, 0, tf}, ImageSize -> Large,
PlotPoints -> 100]
Cheers,
Marco