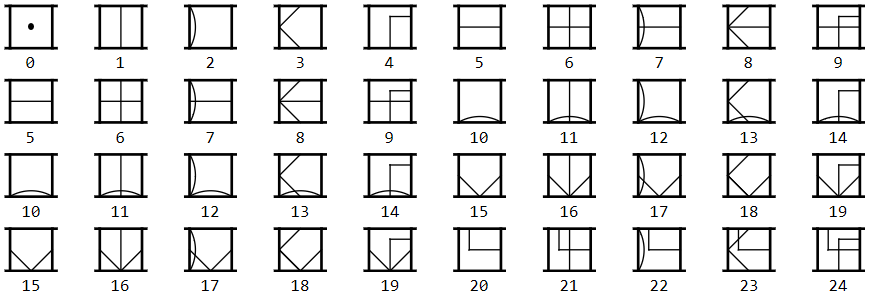
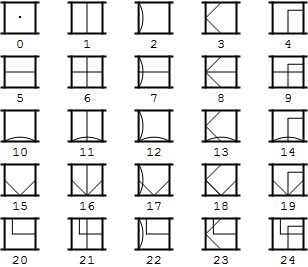
I was recently reminded by a friend about the Myst series of Games from the 1990s. One of my favorite puzzles in that series of games was from the second game in the series, Myst II: Riven. In that game, in order to solve one of the puzzles, you had to literally go back to school to learn how to count using a counting system from an alien culture (called the D'ni). In this case, it was a base-25 counting system. You had to learn the symbols for each digit in the counting system by playing a child's game. It was a great idea that always held my imagination. Using information from a 3rd party site, I was able to write some code in the Wolfram Language to let you visualize how our base-10 numbering system would look in the D'ni numbering system. Its based mainly on graphics to draw the glyphs and then RealDigits to express numbers in the alternate base. I'm sure this can be fledged out more, but I thought it was a fun exercise and thought I would share what I came up with so far.

My background is not number theory so if there are any subtleties I missed, feel free to hash them out here and expand the topic in the comments.

base = {AbsoluteThickness[2], Line[{{-.1, 0}, {1.1, 0}}], 
   Line[{{-.1, 1}, {1.1, 1}}], Line[{{0, 0}, {0, 1}}], 
   Line[{{1, 0}, {1, 1}}]};

grs[0] = {};

grs[1] = {AbsoluteThickness[1], Line[{{0.5, 0}, {0.5, 1}}]};

grs[2] = {AbsoluteThickness[1], 
   Line[Table[{Cos[t] - .86, Sin[t] + .5}, {t, -\[Pi]/6, \[Pi]/6 + 1/20, 
      1/20}]]};

grs[3] = {AbsoluteThickness[1], Line[{{.5, 0}, {0, .5}}], Line[{{0, .5}, {.5, 1}}]};

grs[4] = {AbsoluteThickness[1], Line[{{.5, 0}, {.5, .75}}], 
   Line[{{.5, .75}, {1, .75}}]};

makegr[gr___] := 
 Graphics[{base, gr}, AspectRatio -> .75, PlotRange -> All, ImageSize -> 40]

numpic[0] := makegr[AbsolutePointSize[4], Point[{0.5, 0.5}]]

numpic[num_Integer /; (1 <= num <= 24)] :=
 IntegerDigits[num, 
   5] /. {{i_} :> makegr[grs[i]], {i1_, i2_} :> 
    makegr[GeometricTransformation[grs[i1], 
      RotationTransform[90 Degree, {.5, .5}]], grs[i2]]
   }

DniRealDigits[num_?NumberQ] := Module[{rd, dnirepl},
  rd = RealDigits[num, 25];
  dnirepl = rd /. i_Integer :> numpic[i]
  ]

DniIntegerForm[num_?IntegerQ] := Module[{rd, dnirepl},
  rd = RealDigits[num, 25];
  dnirepl = rd /. i_Integer :> numpic[i];
  Graphics[
   MapIndexed[GeometricTransformation[#[[1]], {#2[[1]], 0}] &, dnirepl[[1]]], 
   ImageSize -> (40*Length[rd[[1]]])]
  ]

Now, with the basic code defined, we can use it with some examples.

Table[With[{n = i*5^1 + j * 5^0}, 
   Grid[{{DniIntegerForm[n]}, {n}}]], {i, 0, 4}, {j, 0, 
   4}] // TableForm

DniRealDigits[N[Pi, 11]]

DniIntegerForm[25]

DniIntegerForm[209]

For convenience, DniIntegerForm has all been bundled up into a Wolfram Function Repository item