Ok, I also do not quite understand what the actual problem is. But it is relatively easy to force Norm to apply to a scalar, if we interpret the scalar as a "one-dimensional vector", i.e. wrapping it in curly brackets. Using the original notebook posted above it looks like this:
f[t_] := 2 Cos[t] + 2 Sin[t] + 4;
FullSimplify[f'[t]/Norm[{f'[t]}]]
which gives
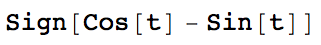
Note, that I needed to enclose f'[t] in "{}"; this is of course quite clumsy, because Abs[] would have achieved the same thing without the curly brackets. Obviously, this is not always one, as can be seen when we plot the function:
Plot[f'[t]/Norm[{f'[t]}], {t, 0, 2 Pi}]
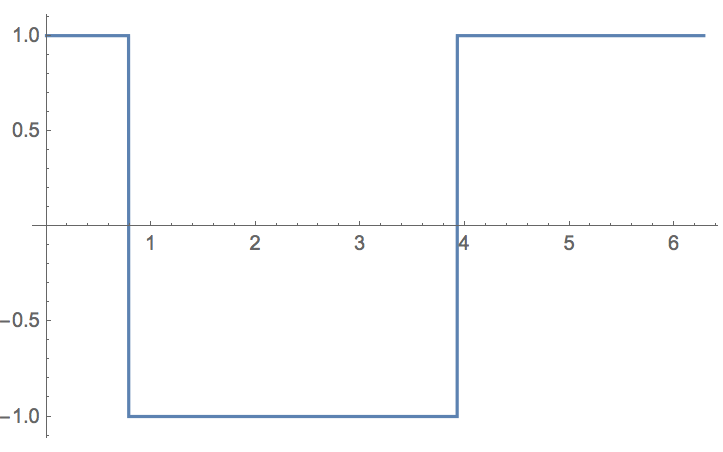
Plotting the nominator and denominator separately, we see that the result makes sense:
Plot[{f'[t], Norm[{f'[t]}]}, {t, 0, 2 Pi}]
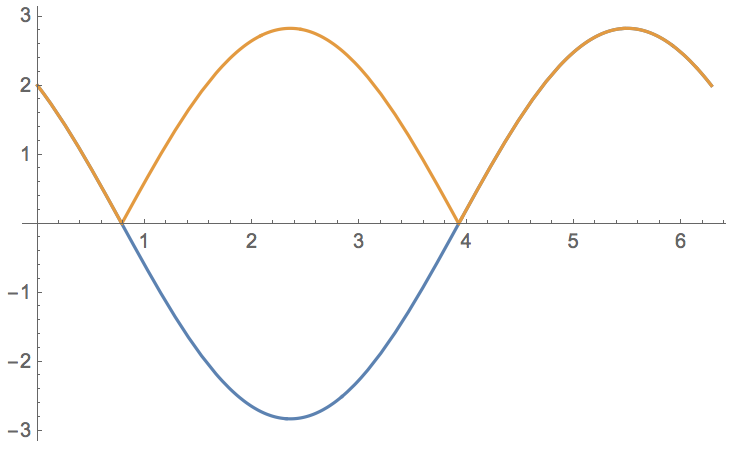
Cheers,
Marco
PS: As I said it would make more sense to use Abs here:
FullSimplify[f'[t]/Abs[f'[t]]]
gives
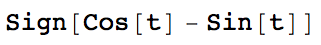
without the use of the artificial curly brackets...