Hi,

It will give me "True" but in fact it isn't! How can i calculate the angle related to the direction?

In fact Mathematica's result is correct and this equation should give True. If you have a look at the documentation of VectorAngle you will see that it uses the standard definition of the angle, which is:

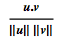
That equation is symmetric in the two vectors, which means that their order does not matter. For example:

VectorAngle[{1, 2}, {2, 1}] == VectorAngle[{2, 1}, {1, 2}]

The function VectorAngle (as its mathematical counterpart above) always give the smaller of the two angles between two planar vectors; that is by definition. If you now look at the example you give, we can plot the three vectors like so:

Graphics[{Arrow[{{0, 0}, {10, 600}}], Arrow[{{0, 0}, {-10, 600}}], Red, Arrow[{{0, 0}, {0, 200}}]}, AspectRatio -> 1]

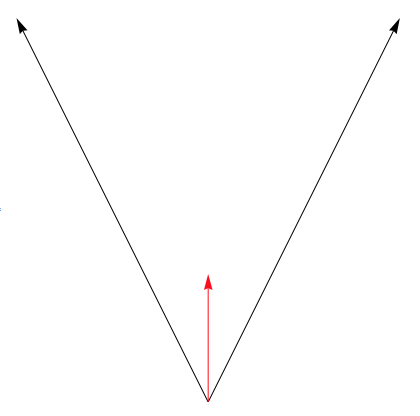
The equation you use calculates the two angles between the black and the red arrow (and always the smallest one!). As the two black vectors are just reflected on the y-axis, these angles are identical which is why Mathematica correctly evaluates

VectorAngle[vector1, secondVector] == VectorAngle[vector2, secondVector]

to true. I guess that what you want is more of an oriented angle, defined as the angle between the ordered pair of vectors in the standard mathematical direction of rotation. Let's assume that there was no function for that in Mathematica, then it would be really easy (modulo some mistakes I might have made) to write one yourself, like so:

orientedAngle[list1_, list2_] := 
 If[(Length[list1] != 2 \[Or] Length[list2] != 2), Message[orientedAngle::baddim], 
 If[Cross[Join[list1, {0}], Join[list2, {0}]][[3]] > 0, VectorAngle[list1, list2], 2 Pi - VectorAngle[list1, list2]]]
orientedAngle::usage = "This function calculates the oriented angle between two 2 dimensional vectors.";
orientedAngle:: baddim = "One of the two vectors has a dimension different from 2.";

If you execute that you get:

orientedAngle[vector1, secondVector] // N
(*0.0166651*)

and

orientedAngle[vector2, secondVector] // N
(*6.26652*)

Now of course you would get:

orientedAngle[vector1, secondVector] == orientedAngle[vector2, secondVector]
(*False*)

You have posted now several time using screenshots rather than inline formulas. That makes it more difficult to help you because we have to type everything in again. It would be very helpful if you could follow the recommendations on how to post in this community.

Cheers,

Marco

PS: In the definition of my function you could of course also use

Det[{list1, list2}]

instead of the cross product, i.e.

orientedAngle[list1_, list2_] := 
 If[(Length[list1] != 2 \[Or] Length[list2] != 2), Message[orientedAngle::baddim], 
  If[Det[{list1, list2}] > 0, VectorAngle[list1, list2], 2 Pi - VectorAngle[list1, list2]]]
orientedAngle::usage = "This function calculates the oriented angle between two 2 dimensional vectors.";
orientedAngle::baddim = "One of the two vectors has a dimension different from 2.";