Wolfram Language Fingerprint Identification and Matching

Introduction
The objective of this study was to create a Mathematica program that would accurately and efficiently compare multiple fingerprints without external hardware. I began my work in August of 2014 as a member of the Wolfram Research Mentorship Program, after having attended the Wolfram Mathematica Camp earlier that summer.
Fingerprint analysis by computational means has grown in significance in modern society; fingerprint matching has been relevant in the field of criminology for a long time, but its applications are growing to complement modern technology, such as the fingerprint recognition functionality of iPhones. Detecting fingerprints accurately, however, requires either sensitive and expensive specialized fingerprinting machines or specialized technology unavailable to the public.
Thus far, there are extremely few applications that allow users to acquire and compare their fingerprints easily. In my research, I examined the ability of Mathematica and its image processing functionality to compare and analyze fingerprints extracted from live photographs.
Methods/Experimentation
Acquisition of Fingerprints for Testing
Fingerprints for this research were acquired from several locations. These include: extracted Fingerprints from OnyxKit application, VeriFinger Fingerprint Database, FVC2 (Fingerprint Verification Contest) Sample Database, and CASIA-Fingerprint V5 Biometrics Ideal Test. All downloaded Fingerprint sets are free, but require registration. When live testing was done, fingerprints were taken from myself, close family, as well as friends.
Pre-Printed Fingerprint Analysis
- ImageKeyPoints (Testing on Pre-Printed Fingerprints)
After investigation into several other methods of fingerprint matching, the Mathematica commands ImageKeyPoints and ImageCorresponding Points were determined to be the best method of comparing fingerprints.
ImageKeyPoints is a Mathematica command that uses the SURF (Speeded Up Robust Features) algorithm that uses a complex blob detector to identify points within the image that stood out in contrast to surrounding points, which are analyzed using the Haar wavelet sum. The command outputs coordinates of points which are determined to be sufficiently unique or distinct.
The following code and image are an illustration of a set of key points on a Pre-Printed Fingerprint from the VeriFinger Fingerprint Database:
HighlightImage[FP1, ImageKeypoints[FP1], "HighlightColor" -> Yellow]

The number of key points for an image was quantified using the simple command:
Length[ImageKeyPoints[FP1]]
Over every Pre-Printed Database, the number of Key Points was quantified to ensure that there was no significant difference within a set of images from the same database, as this number is used in a later calculation. When comparing a set of fingerprints, I found that there was no statistically significant difference within sets with p < .05.
- ImageCorrespondingPoints (Testing on Pre-Printed Fingerprints)
ImageCorrespondingPoints (ICP) is a similar command to ImageKeyPoints; the purpose of ICP is to identify points in common between two images. These Corresponding Points are selected from the set of Key Points. A sample snippet of code as well as an image of ICP on a pair of images of a fingerprint extracted from OnyxKit application.
Corresponding Points highlighted from two different Fingerprints from the Same Individual
Images = {FP1, FP3}; matches =
ImageCorrespondingPoints @@ images; MapThread[
Show[#1, Graphics[{Yellow,
MapIndexed[Inset[#2[[1]], #1] &, #2]}]] &, {images, matches}]

Corresponding Points highlighted from two different Fingerprints from Different Individuals

The number of Corresponding points for a pair of images was quantified using the simple command:
Length[ImageCorrespondingPoints[FP1, FP2]]
- Determining the Threshold
A percentage similarity between two fingerprints was calculated as follows:
(2 NumberofCorrespondingPoints[FP1, FP2])/(NumberofImageKeyPoints[FP1] + NumberofImageKeyPoints[FP2])
This is essentially equal to the number of points in common between the two images divided by the average number of key points.
This %Similarity was calculated among thousands of pairs of images from the same finger of the same individual, as well as fingerprints from different individuals. These fingerprints were captured using OnyxKit. The key of this project was to find the proper %Similarity (threshold) with which we can say that if the calculated %Similarity > Threshold, then the fingerprints are the same, and if %Similarity < Threshold, then the fingerprints are different. The Threshold determined for pre-printed fingerprints was determined to be the surprisingly and extremely small, 1.5%.
Such a low threshold is a key indicator that our method for comparing fingerprints is very accurate in predicting if fingerprints are different, allowing us to set a low threshold to capture fingerprints from the same individual that may have a low number of Corresponding Points.
A key component of the analysis was determining the proper KeyPointStrength in the ImageCorrespondingPoints. KeyPointStrength is an option of ICP, which alters the requirements for a point to be considered a Key Point. An increase in KeyPointStrength corresponds to a decreased number of Key Points found. The values for KeyPointStrength Testing included KSP = .001, .0004, .0005, .00075. The code for KSP was:
ImageCorrespondingPoints[FP1, FP2, KeypointStrength -> ____ ]
The conclusion was that at a KeypointStrength of .0004, the results were optimal: for two of the same fingerprints, the certainty of a match = 85%. For two different Fingerprints, the certainty of no match is 86%. The value of KSP was eventually changed when testing on live finger images, when a similar analysis was repeated.
Live Fingerprint Analysis
- Extraction of Finger from Image
All of the prior analysis set the precedent for the investigation into live fingerprints. The purpose of this project was to allow a user to upload multiple images of fingers taken simply by a camera or phone without necessity of specialized technology.
Therefore, after pictures of fingers were uploaded to the program, a system had to be discovered to isolate only the finger from a complete image. This presents a significant Image Processing and Manipulation problem.
I proposed three solutions this problem:
(1) Pure Image Manipulation (No Preparation Required)
In this method, a picture of a fingerprint is taken without regard to the background. The purpose of this code is to be able to extract a fingerprint from the uploaded image. This extracted fingerprint should be surrounded by a black background to which image key points can be applied properly on.
FPExtract[k_] :=
ImageCrop[
ImageSubtract[k,
ColorNegate[
DeleteSmallComponents[
MorphologicalBinarize[
ColorCombine[ColorSeparate[k], "LAB"], {.65}]]]]]
Extraction Results:
Original Image:
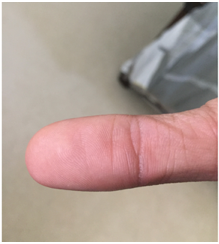
Extracted Image:
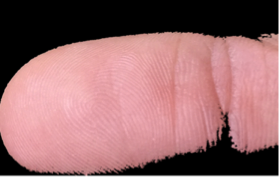
(2) Uniform Background Method
In this method, the background is taken into account. Here, the image of the fingerprint must be taken with a purely uniform background. The results of this extraction are shown below:
FPExtracted1 =
ImageMultiply[
FP1 SelectComponents[FillingTransform@Binarize[FP1],
"Area", -1]];
FPExtractedFinal = ImageSubtract[FP1, FPExtracted1]
Original Image:
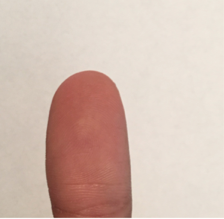
Extracted Image:

(3) Flash Photography
A slightly unique method was discovered when I realized that simply turning flash on may be extremely effective. This was motivated by my desire to use a form of morphological binarize; this requires a contrast in the lighting of the finger vs the lighting of the background. Therefore, I reasoned, when the flash is aimed on the finger when a photograph is being taken, that should facilitate the use of a binarize command to extract the fingerprint.
FPExtract[a_] :=
ImageCrop[
ImageSubtract[a, ColorNegate[DeleteSmallComponents[Binarize[a]]]]]
Original Image:
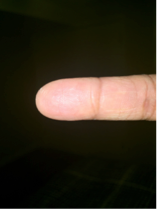
Extracted Image:
Conclusion
After large amounts of testing, it was determined that with regard to accuracy as well as practicality, the best method would be the method 3 using flash photography. The other methods are included here to reveal the potential for better solutions, especially method 1, which if improved, would be the ideal method.
The threshold for this portion of the project was set using the exact same method as previously described. A large set of pairs of fingerprints using method 3 was analyzed to determine the ideal threshold. It was determined that the ideal threshold to maximize correct interpretations of pairs of fingerprints was approximately 1.2%.
- Reference Fingerprints and Probability Calculations
Most standard fingerprint matching software requires a number of reference fingerprints. This means, that give an input fingerprint FP1, and reference fingerprints FP2, FP3, ...., FPN, the input fingerprint is compared to each reference fingerprint to increase the accuracy of the final conclusion. These reference fingerprints can either be from a different individual from the input or from the same individual, and a decision is thus made.
It is critical to determine the probability of making an accurate conclusion during this process. For example, as the number of reference fingerprints increases, the probability of making a correct conclusion increases.
Probability calculations were done using conditional Bayesian probability. The general formula for this is:
P(B|A) = (P(B)P(A|B)) / (P(B)P(A|B) + P(B^c)P(A|Bc)
In this computation, certain information needs to be known prior to computation: this includes the general probability that a known correct match will be interpreted as a match. This was determined to be 90%. It also was needed to be known what the probability of a known invalid match being interpreted as a valid match. This was determined to be 11%. These numbers were acquired after analyzing thousands of pairs of fingerprints.
There are two situations in which this is applied:
(1) Probability of Match
In this scenario, B= Probability of Correct Conclusion, and A = Number of Matches Found
The following code computes the probability of a conclusion of a match, given that there are MatchCount number of determined matches that are greater than the threshold.
ProbabilityofSame =
((.90)^MatchCount (1 - .90)^(Length[t] - MatchCount))/
(((.90)^MatchCount (1 - .90)^(Length[t] - MatchCount)) + ((.11)^MatchCount (1 - .11)^(Length[t] - MatchCount)))
(2) Probability of Invalid Match
In this scenario, B= Probability of Correct Conclusion, and A = Number of Matches Found
The following code computes the probability of a conclusion of a match, given that there are MatchCount number of determined matches that are greater than the threshold.
ProbabilityofSame =
((.90)^MatchCount (1 - .90)^(Length[t] - MatchCount))/
(((.90)^MatchCount (1 - .90)^(Length[t] - MatchCount)) + ((.11)^MatchCount (1 - .11)^(Length[t] - MatchCount)));
- Final Determination of Results
The final conclusion of whether the result is a match or an invalid match is determined using the probabilities computed above. If the probability of a valid match is greater than the probability of an invalid match, then the result is a match, and vice versa. The final conclusion is printed as well as calculated probability that the result is correct.
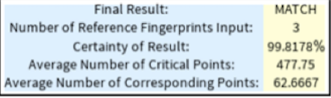
Conclusion:
Through this project, I have explored the use of Mathematica to identify and match fingerprints. A number of different methods were used throughout this project, but after significant data analysis, the method through Key Point analysis was determined to be the most effective. As a result, users should be able to input live photographed fingerprints and analyze them.
Beyond its immediate results, this project also has several implications for future study. A significant amount of time of this study, although not included in this report, was devoted to the study of traditional Fingerprint matching techniques, such as ridge bifurcations, edges, etc. The code developed in this avenue was not further pursued, as the key points analysis was more practical, but there is room here for much further investigation. Improvements in the image processing would also be highly relevant, as improved fingerprint extraction would increase the significance of results tremendously. Finally, more data in even larger quantities would be helpful in confirming the current threshold, or establishing a new, final one.
Acknowledgements:
I would primarily like to thank Dr. Rowland for his mentorship and assistance throughout the entire course of the project. I would also like to thank Ms. Kimball for her involvement and assistance near the end of the project, as well as the Onyx and the various Fingerprinting Databases for allowing my use of their samples. Finally, I would like to thank my parents for their constant support.
Final Code
This is the code the deploys the program directly to the cloud
CloudDeploy[FormFunction[{
{{"y", "Input Fingerprint"} ->
"Image", {"x", "Number of Reference Fingerprints"} -> {"1", "2",
"3", "4"}},
Function[
Table[{"a" <> ToString[i],
"Reference Fingerprint " <> ToString[i]} -> "Image",
{i, ToExpression[#x]}]
]},
Module[{RefFP, FPAnalysis, MatchCount, NumberofCorrespondingPoints,
NumberofInputKeyPoints, NumberofReferenceKeyPoints,
ProbabilityofSame, ProbabilityofDifferent, FPAnalysisModified,
FPAnalysisFinalModified, w, u, q, n, t, b},
t = Table[ #["a" <> ToString[j]], {j, ToExpression[#x]}];
b = ImageRotate[#y, 3 Pi /2];
t = Table[ImageRotate[t[[i]], 3 Pi/2], {i, 1, Length[t]}];
NumberofInputKeyPoints =
Length[ImageKeypoints[b]];
NumberofReferenceKeyPoints =
Table[
Length[
ImageKeypoints[t[[u]]]],
{u, 1, Length[t]}];
NumberofCorrespondingPoints =
Table[
Length[
Flatten[
ImageCorrespondingPoints[b, t[[q]]], 1]],
{q, 1, Length[t]}];
FPAnalysis =
Table[{
MapThread[
Show[#1,
Graphics[{Yellow,
MapIndexed[Inset[#2[[1]], #1] &, #2]}]] &, {{b, t[[n]]},
ImageCorrespondingPoints @@ {b, t[[n]]}}],
Row[{N[
200 NumberofCorrespondingPoints[[n]]
/ (Plus[NumberofInputKeyPoints,
NumberofReferenceKeyPoints[[n]]
])], "%"}],
Which[
200 NumberofCorrespondingPoints[[
n]]/ (Plus[NumberofInputKeyPoints,
NumberofReferenceKeyPoints[[n]]]) > 1.2, "Match",
200 NumberofCorrespondingPoints[[
n]]/ (Plus[NumberofInputKeyPoints,
NumberofReferenceKeyPoints[[n]]]) < 1.2,
"Invalid Match"]},
{n, 1, Length[t]}];
MatchCount =
(Length[t] -
Total[StringCount[Flatten[FPAnalysis][[4 ;; ;; 4]],
"Invalid Match"]]);
ProbabilityofSame =
((.90)^
MatchCount (1 - .90)^(Length[t] - MatchCount) ) / (((.90)^
MatchCount (1 - .90)^(Length[t] - MatchCount) ) + ((.11)^
MatchCount (1 - .11)^(Length[t] - MatchCount) ));
ProbabilityofDifferent =
((.11)^
MatchCount (1 - .11)^(Length[t] - MatchCount) )/ (((.90)^
MatchCount (1 - .90)^(Length[t] - MatchCount) ) + ((.11)^
MatchCount (1 - .11)^(Length[t] - MatchCount) ));
FPAnalysisModified =
FPAnalysis /.
"Match" ->
Item[Style["Match", FontWeight -> Bold, FontFamily -> Times,
FontSize -> 16], Background -> Green];
FPAnalysisFinalModified =
FPAnalysisModified /.
"Invalid Match" ->
Item[Style["Invalid Match", FontWeight -> Bold,
FontFamily -> Times, FontSize -> 16], Background -> Red];
Grid[
{
{
Framed[
Grid[{{"Wolfram Mathematica Fingerprint Matching Research:",
"Tushar Dwivedi"}, {"Final Result:",
If[ProbabilityofSame > ProbabilityofDifferent, " MATCH ",
" INVALID MATCH "]}, {
"Number of Reference Fingerprints Input:",
Length[t]}, {"Certainty of Result:", If[ProbabilityofSame >
ProbabilityofDifferent,
StringJoin[ToString[100 ProbabilityofSame], "%"],
StringJoin[ToString[100 ProbabilityofDifferent], "%"]]},
{ "Average Number of Critical Points:",
N[Mean[Join[
NumberofReferenceKeyPoints, \
{NumberofInputKeyPoints}]]]}, {
"Average Number of Corresponding Points:",
N[ Mean[NumberofCorrespondingPoints]]}},
Background -> {{1 -> LightBlue, 2 -> LightYellow}, None}]]},
{Insert[
ReplacePart[
Grid[
Join[
{{Style["Corresponding Points Display", FontSize -> 16,
FontFamily -> Times], SpanFromLeft,
Style["Threshold: 1.2%", FontSize -> 16,
FontFamily -> Times],
Item[If[ProbabilityofSame >
ProbabilityofDifferent
Style["Result: MATCH", FontFamily -> Times,
FontWeight -> Bold],
Style["Result: INVALID MATCH", FontFamily -> Times,
FontWeight -> Bold]],
Background ->
If[ProbabilityofSame > ProbabilityofDifferent, Green,
Red]] }},
Flatten /@ FPAnalysisFinalModified]
],
1 -> Prepend[
First[
Grid[
Join[
{{Style["Corresponding Points Display", FontSize -> 16,
FontFamily -> Times], SpanFromLeft,
Style["Threshold: 1.2%", FontSize -> 16,
FontFamily -> Times], Item[If[ProbabilityofSame >
ProbabilityofDifferent,
Style["Result: MATCH", FontFamily -> Times,
FontWeight -> Bold],
Style["Result: INVALID MATCH", FontFamily -> Times,
FontWeight -> Bold]],
Background ->
If[ProbabilityofSame > ProbabilityofDifferent,
Green, Red]] }},
Flatten /@ FPAnalysisFinalModified]
]
],
{Style["Fingerprint Input", FontSize -> 16 ,
FontWeight -> Bold, FontFamily -> Times],
Style["Reference Fingerprint", FontSize -> 16 ,
FontWeight -> Bold, FontFamily -> Times],
Style["Match Strength", FontSize -> 16 ,
FontWeight -> Bold, FontFamily -> Times],
Style["Result", FontSize -> 16 , FontWeight -> Bold,
FontFamily -> Times]}]],
{Dividers -> All, Spacings -> 1.5` {1, 1}}, 2]},
{Framed@Text
[Style[
" The input fingerprint was paired with each of the input \
reference fingerprints, and Wolfram Mathematica was used to identify \
critical points in all input fingerprints. These critical points \
include bifurcations (where the fingerprint line branches), ridge \
endings (where the fingerprint line stops), and various other \
minuitae. The major premise of fingerprint testing is to compare the \
critical points in two fingerprints, and find how many of these \
minuitae are the same. Therefore, the number of critical points in \
the input that corresponded to critical points in the reference \
fingerprint was calculated for each pair. The Match Strength is \
calculated by finding the percent of the average number of critical \
points that correspond between the pair of fingerprints. After \
testing thousands of pairs of fingerprints, the threshold for a Match \
Strength to qualify as a match was set at 1.2%. Thus, if the match \
strength was greater than 1.2% for a pair, then that pair of the \
input and reference was determined to be a match. To get the overall \
determination of a match or invalid match, Bayesian probability was \
used to calculate the certainty of being a match based on the number \
of matches or invalid matches found between the input fingerprint and \
each of the reference fingerprints.", TextAlignment -> Left,
FontSize -> 14, FontFamily -> Times,
LineSpacing -> {1.67, 0}], Background -> LightGreen]}}
]
] &, "PNG",
AppearanceRules -> <|
"Title" -> "Wolfram Fingerprint Identification",
"Description" -> "Match your fingerprints!"|>],
Permissions -> "Public"]