Im not sure that you understand the problem. Physics dont limit the value of F. It can be whatever the experimenter chooses it to be, >0, =0, <0, in any direction.
Please refer to the bookshelf figure below.
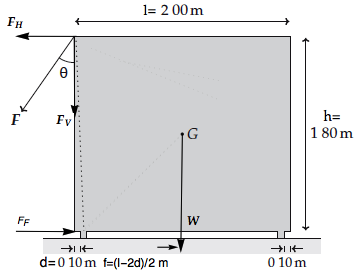
Computed F value is actually an advice to experimenter that with given choice of ? he should apply at least force F if he wants the bookshelf to start gliding over the floor. Therefore F = {Undefined} for 0 <= ? <= ArcTan[Subscript[[Mu], S] the bookshelf will newer glide in this ? range. F should be Subscript[[Mu], S] Subscript[F, N] for ArcTan[Subscript[[Mu], S] < ? <= 90°.
Physics do limit value of Subscript[F, F]. It must be non-negative. It is the friction force and as such it cannot be negative. The lowest value it can have is 0. The condition is:
Subscript[F, F] := If[Subscript[\[Mu], S] Subscript[F, N] >= 0, Subscript[\[Mu], S] Subscript[F, N], 0]
where Subscript[[Mu], S] is friction coefficient and Subscript[F, N] is normal force:
Subscript[F, N] := Subscript[F, V] + W := 1500 + F Cos[\[Degree] \[Theta]]
in this particular experiment. Whenever Subscript[F, N] gets negative because of Cos[?] or because of F (the bookshelf could be pushed instead of dragged) then Subscript[F, F] shall be 0 and F should be {Undefined}
If you look at the solution produced by Solve[] in my original post then you can see the condition for F to be computed:
(Sin[?] > 2/5 Cos[?] && Cos[?] > 0) ||
(Sin[?] < 0 && Cos[?] > 0) ||
(Sin[?] < 2/5 Cos[?] && Cos[?] < 0) ||
(Cos[?] < 0 && Sin[?] > 0)
The first and the second test should test for Cos[?] >= 0 then the solution would be flawless.
In my opinion there is a bug somewhere in Mathematica.
Thanks