ll[StNdRd, CreateTemplate]
StNdRd[n_String] :=
If[IntegerQ[ToExpression[n]], StNdRd[ToExpression[n]], ""]
StNdRd[n_Integer] :=
If[3 < n < 21, "th",
Switch[Mod[n, 10], 1, "st", 2, "nd", 3, "rd", _, "th"]]
CreateTemplate[time_: Now] :=
Module[{t, top, middle, dayofyear, totaldays, week, dayofweek,
ordinal, bottom2, Quarterstart, dayofquarter, Quarterend,
daysinquarter}, t = Take[DateList[time], 3];
dayofyear = DateValue[t, "ISOYearDay"];
totaldays = If[LeapYearQ[t], 366, 365];
week = DateString[t, "WeekShort"];
dayofweek = DateString[t, "ISOWeekDay"];
top = {Style[DateString[t, {"Year", "Month", "Day"}], Bold],
Row[{ToString[dayofyear], "/", ToString[totaldays - dayofyear]}],
Row[{Style["WK" <> week, Red, Bold],
Style["-" <> dayofweek, Bold]}]};
top = {Row[top, " | "], SpanFromLeft};
ordinal = StNdRd[DateValue[t, "Day"]];
middle = {Style[
DateString[
t, {"DayName", ", ", "MonthName", " ", "DayShort", ordinal,
", ", "Year"}], White], SpanFromLeft};
Quarterstart = Take[DateList[t], 2];
Quarterstart = {First[Quarterstart],
Floor[Last[Quarterstart] - 1, 3] + 1, 1};
Quarterend = Quarterstart;
Quarterend[[2]] += 3;
Quarterend = DateList[Quarterend];
daysinquarter =
QuantityMagnitude[DateDifference[Quarterstart, Quarterend], "Day"];
dayofquarter =
QuantityMagnitude[DateDifference[Quarterstart, t, "Day"], "Day"] +
1;
bottom2 =
Column[{Row[{DateString[t, {"Quarter"}] <>
StNdRd[DateValue[t, "Quarter"]] <> " Quarter ", dayofquarter,
"/", daysinquarter - dayofquarter}],
Row[{"(", daysinquarter, " Days", " / 13 Weeks)"}]}, "Center"];
Grid[{top, middle, {Null, bottom2}}, Frame -> All,
Background -> {None, {None, Black, None}}]]
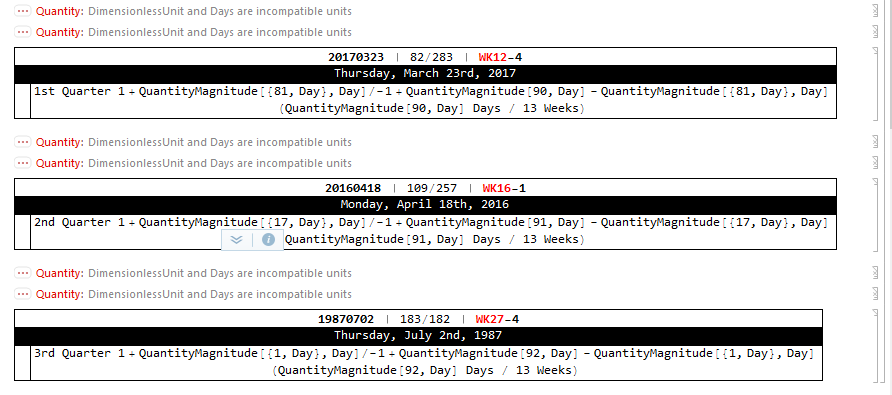
CreateTemplate[]
CreateTemplate[{2016, 4, 18}]
CreateTemplate[{1987, 7, 2}]
Which gives me the example for today as...
Example by Hans Michel, when I use it from 11.1
SetSystemOptions["DataOptions" -> "ReturnQuantities" -> False];
ISOWeek[x_] :=
Module[{d2},
d2 = DateList[{ToExpression[
DateString[
DatePlus[
x, {(-(Flatten[
Position[{"Sunday", "Monday", "Tuesday", "Wednesday",
"Thursday", "Friday", "Saturday"},
DateString[DatePlus[x, {-1, "Day"}], {"DayName"}],
1]])[[1]] + 4), "Day"}], "Year"]], 1, 3, 0, 0, 0}];
IntegerPart[(DateDifference[d2, x] +
Flatten[Position[{"Sunday", "Monday", "Tuesday", "Wednesday",
"Thursday", "Friday", "Saturday"},
DateString[d2, {"DayName"}], 1]][[1]] + 5)/7]];
ISODay = Function[{date},
Flatten[Position[{"Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"},
DateString[date, {"DayNameShort"}], 1]][[1]]];
Grid[{{Item[
Style[DateString[DateList[], {"Year", "", "Month", "", "Day"}],
FontFamily -> "Arial Black", FontWeight -> "Black",
FontSize -> 32], Alignment -> Center],
Item[Style[
StringJoin[
ToString[
IntegerPart[DateDifference[{First[DateList[]]}, DateList[]]]],
" / ",
ToString[
IntegerPart[
DateDifference[DateList[], {Plus[First[DateList[]], 1]}]]]],
FontSize -> 28, FontFamily -> "Arial", FontWeight -> Bold],
Alignment -> Center],
Item[Style[
Row[{Style[StringJoin["WK", ToString[ISOWeek[DateList[]]]], Red],
Style[StringJoin["-",
ToString[
NumberForm[ISODay[DateList[]],
NumberPadding -> {"0", ""}]]], Black]}], FontSize -> 30,
FontFamily -> "Arial Black", FontWeight -> Bold],
Alignment -> Center]}, {Item[
Style[DateString[
DateList[], {"DayName", ", ", "MonthName", " ", "Day", "th, ",
"Year"}], FontSize -> 40, FontFamily -> "Calibri",
FontWeight -> Bold, FontColor -> White, Background -> Black],
Alignment -> Center, Background -> Black], SpanFromLeft,
SpanFromLeft}, {Row[{Item[
Style["Spring 30/63 (2nd)", FontSize -> 24,
FontFamily -> "Arial", FontWeight -> Bold],
Alignment -> Center], Spacer[50],
Item[Style[
StringJoin[DateString[DateList[], "Quarter"], "nd",
" Quarter ", "18/73 (3rd)"], FontSize -> 24,
FontFamily -> "Arial", FontWeight -> Bold],
Alignment -> Center]}, Alignment -> Center, Frame -> False],
SpanFromLeft, SpanFromLeft}}, Frame -> True,
FrameStyle -> Thickness[5], Spacings -> {2, 5}]
Which gives me the example for today as...
This is what I have been wondering, because I am not sure what will be the most efficient way to create the most accurate templet possible, using the wolfram language, but after reading the most recent post by Stephen Wolfram "The R&D Pipeline Continues: Launching Version 11.1" and updates made to "DateObject" function and granular dates could we use the same thing, or is there something similar for seasons, for timing a season precisely, which as you can see from the two examples we have not yet been able to accomplish. Yet with a more precise time period wouldn't we be able to have the season start and end precisely when spring, in this case starts and ends. Yet in the two examples we could not get the season to work, and personally I would not have a clue how to best accomplish this without a more precise function. This and a more accurate frame as shown in my original post is all that is standing in the way of using the Wolfram Langue over the way I have been doing it for years in word, and would save me a tremendous amount of time and frustration.
Thanks in advance, for any help from the community.
