Hi Jan,
most likely Wolfram|Alpha used this:
ArcLength[{\[Theta], Sin[\[Theta]]}, {\[Theta], 0, 3 Pi/2}] // N
which evaluates to 5.7303. That does actually make sense if you ask about the length of the curve, which should be larger than 3. Here is a simple example which substitutes the Sine curve by three straight lines (or two depending on your philosophical point of view):
Show[ParametricPlot[{\[Theta], Sin[\[Theta]]}, {\[Theta], 0, 3 Pi/2}],
Graphics[Line[{{0, 0}, {Pi/2, 1}, {Pi, 0}, {3 Pi/2, -1}}]]]
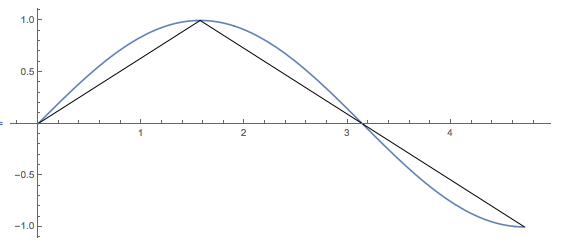
Clearly, the black line is shorter than the sine curve. And the total length of the black lines is:
ArcLength[Line[{{0, 0}, {Pi/2, 1}, {Pi, 0}, {3 Pi/2, -1}}]] // N
which evaluates to 5.58629 and is a lower bound to the length of the sine curve. You are doing something quite different. You look at the vertical motion only. In a two dimensional plot this corresponds to three stretches of lines each of length 1. So you are doing this:
Total[ArcLength /@ (Line /@ Partition[Table[{0, Sin[\[Theta]]}, {\[Theta], 0, 3 Pi/2, Pi/2}], 2, 1])]
which gives 3.
Cheers,
M.
PS: In general if you want to know what Wolfram|Alpha does this is a useful approach: Type in an equal sign at the beginning of the input line in Mathematica and then use the same input you used for Wolfram|Alpha:

This evaluates to

which shows what Wolfram|Alpha does. Note that this function is equivalent to my ArcLength function.