Message Boards Message Boards

Improve this flying graph using GeometricTransformation?

It was a small experiment for getting a better understanding using rotationtransform. Below I show you mine result.

data = Flatten[Table[{x, y, x^2 - y^2}, {x, -3, 3}, {y, -3, 3}], 1];

FG = Table[
  MapAt[GeometricTransformation[#, 
     RotationTransform[t Pi/8, {0, 0, 1}]] &, 
   ListPlot3D[data /. {x_, y_, z_} -> {x, y, z*t}, 
    PlotRange -> {{-6, 6}, {-6, 6}, {-65, 65}}, Boxed -> False, 
    PlotStyle -> Directive[Opacity[.5], Green], Mesh -> 5, 
    MeshStyle -> White, AxesOrigin -> {0, 0, 0}, ImageSize -> 800, 
    PlotLabel -> "Flying Graph", 
    Lighting -> {{"Directional", Green, {{0, 0, 10}, {0, 0, 0}}}}, 
    ViewPoint -> {10, -2, 1}], {1}], {t, -8, 8, 1}]

enter image description here

Export["FlyingGraph.GIF", FG, "DisplayDurations" -> 1];

Do you have suggestions for improvement?
POSTED BY: Michiel van Mens
1 Reply
Sort By:

Hi,

The surface you're working with and the methods you're investigating are really interesting topics. General suggestions I can think of:

You could experiment with different methods of generating the hyperbolic paraboloid,

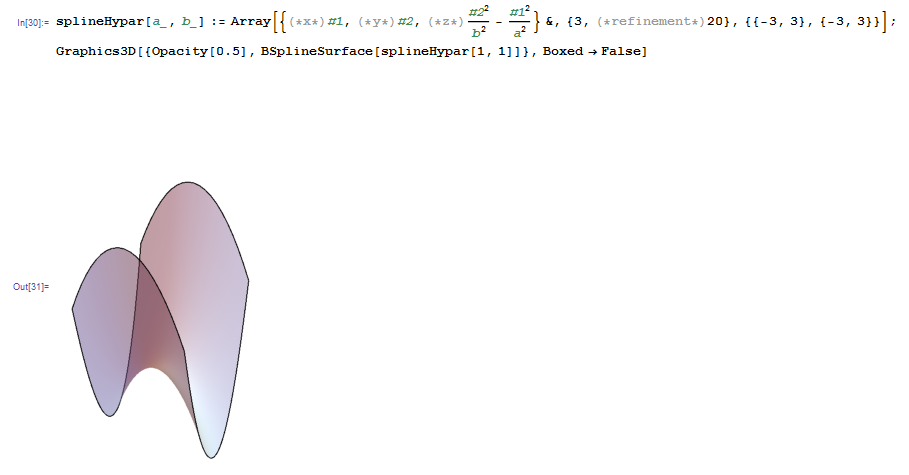
splineHypar[a_, b_] := Array[{(*x*)#1,(*y*)#2,(*z*)#2^2/b^2 - #1^2/a^2} &, {3,(*refinement*)20}, {{-3, 3}, {-3, 3}}];
Graphics3D[{Opacity[0.5], BSplineSurface[splineHypar[1, 1]]}, Boxed -> False]

enter image description here

Use Manipulate to play with the surface and the rotation parameter

Manipulate[
 GeometricTransformation[#, 
    RotationTransform[\[Theta], {0, 0, 1}]] & /@ 
  Graphics3D[{Opacity[0.5], 
    BSplineSurface[
     splineHypar[a, b]]}], {\[Theta], -\[Pi], \[Pi], \[Pi]/20}, {a, 1,
   2, 0.05}, {b(*a*), 1, 2, 0.05}]

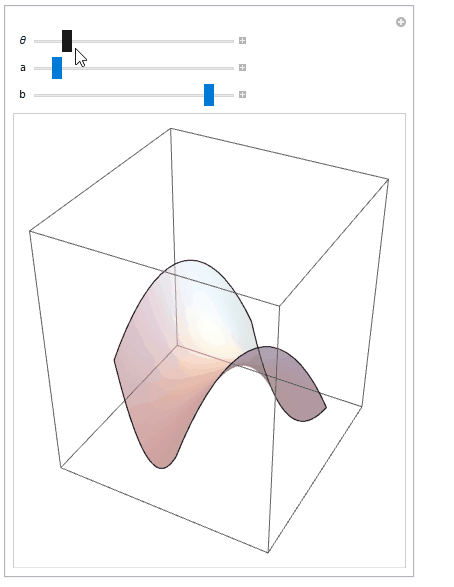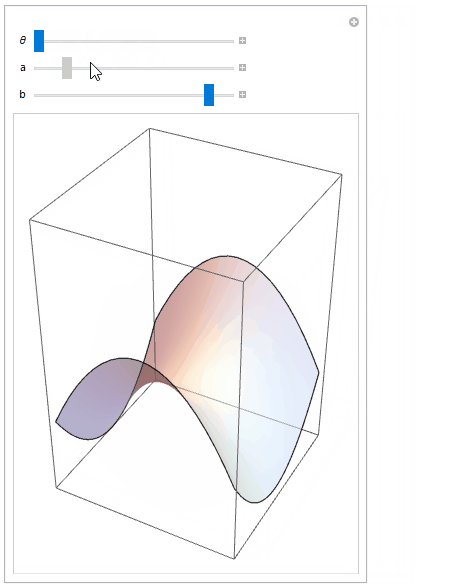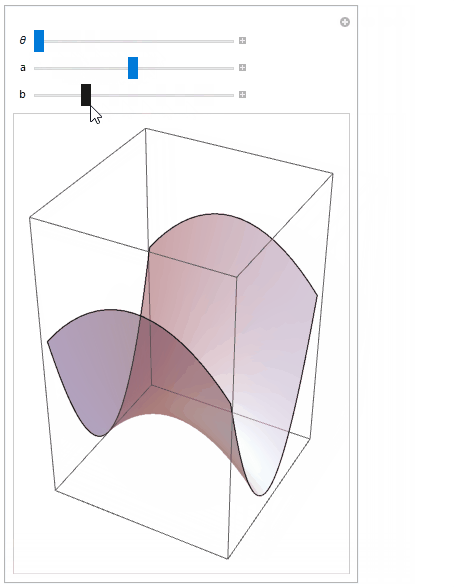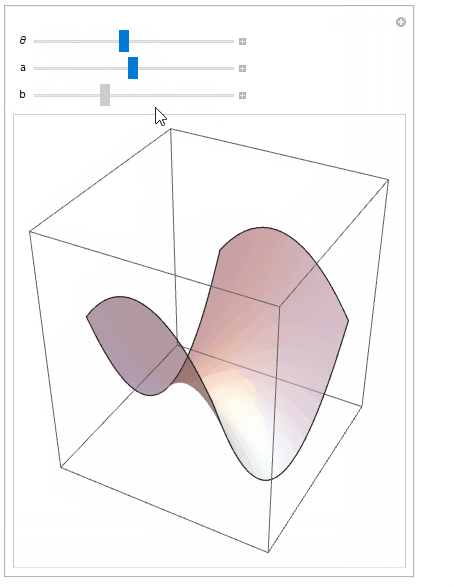
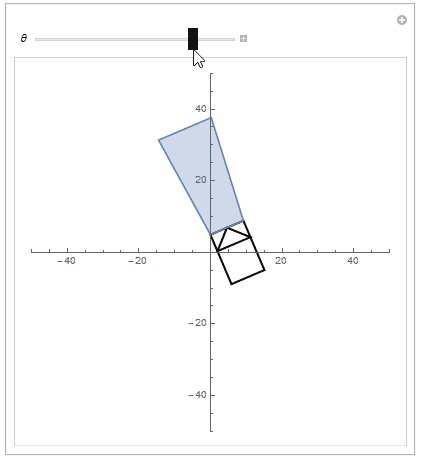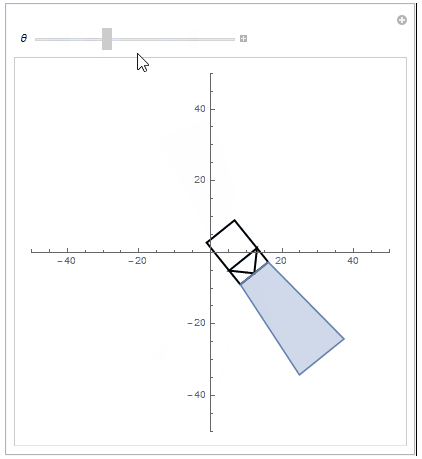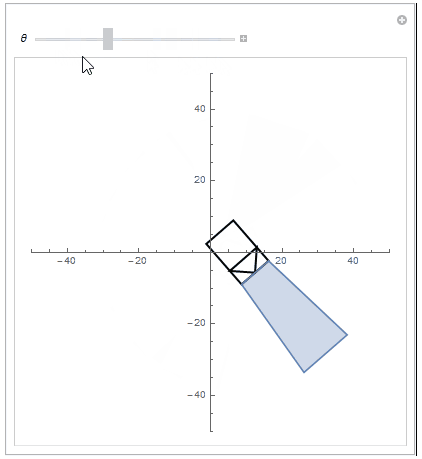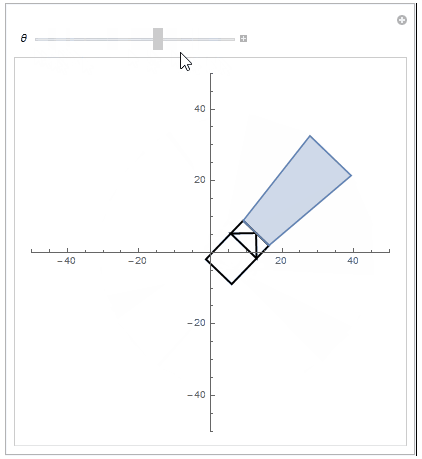
enter image description here

If you want to do more things with Geometric/Rotation Transform, try combining multiple graphic objects,

Manipulate[
 Show[{
   (*car=*)Graphics[{
       EdgeForm[Thick], White,
       GeometricTransformation[
        Rectangle[{#1, #2 - (#4 1)}, {#1 + (#4 3), #2 + (#4 1)}], 
        RotationTransform[#3, {#1 + (#4 1.5), #2}]],
       GeometricTransformation[
        Triangle[{{#1 + (#4 2), #2 + (#4 1)}, {#1 + (#4 2), #2 - (#4 \
1)}, {#1 + (#4 3), #2 }}], RotationTransform[#3, {#1 + (#4 1.5), #2}]]
       }] &[p[[1]], p[[2]], \[Theta], 5],
   RegionPlot@
      TransformedRegion[
       Polygon[{{p[[1]] + 15, p[[2]] - 5}, {p[[1]] + 15, 
          p[[2]] + 5}, {p[[1]] + 15 + #1, 
          p[[2]] + 5 + (#1/#2)}, {p[[1]] + 15 + #1, 
          p[[2]] - 5 - (#1/#2)}}], 
       RotationTransform[\[Theta], {p[[1]] + (15/2), p[[2]]}]] &[30, 
    10]
   }, Axes -> True, PlotRange -> {{-50, 50}, {-50, 50}}],
 {{\[Theta], 0, \[Theta]}, -\[Pi], \[Pi]}
 ]

enter image description here

Hope this helps,

Ben
POSTED BY: Benjamin Goodman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract