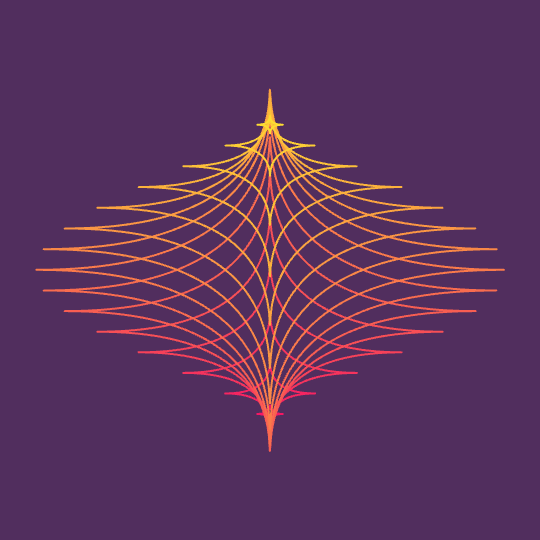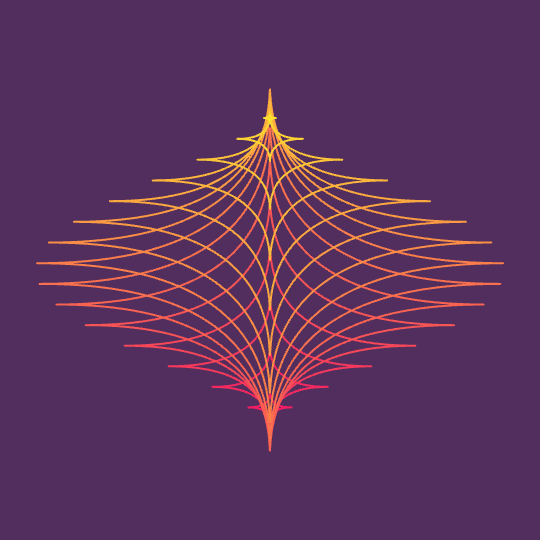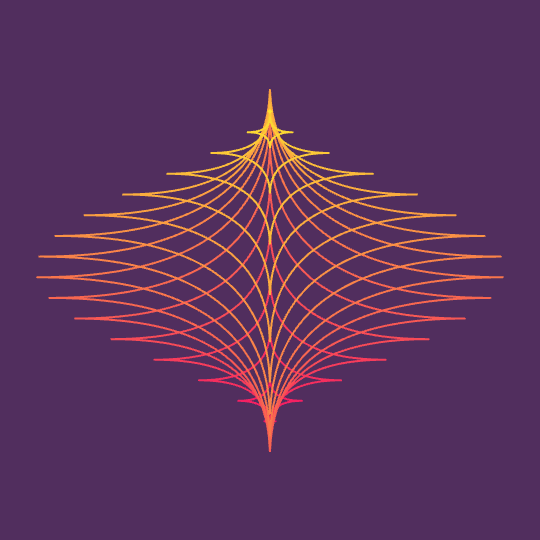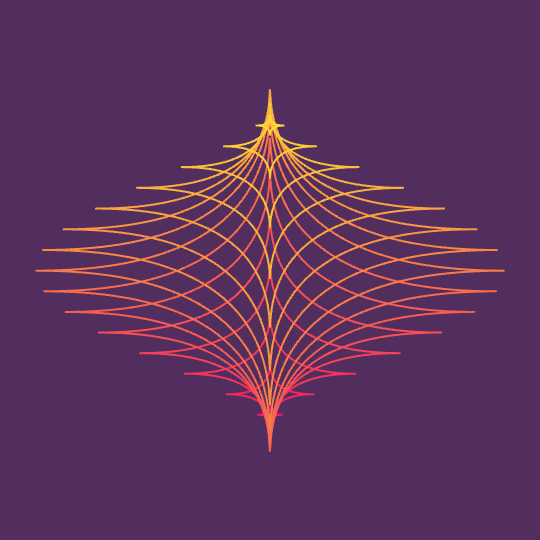
Phoenix

In the spirit of Separation Anxiety and Shifting Lands, some contours of the surface $\sqrt{|x|} + \sqrt{|y|} + z^2 = 1$. The perspective plays some interesting tricks, I think. Here's a more traditional view of the surface:

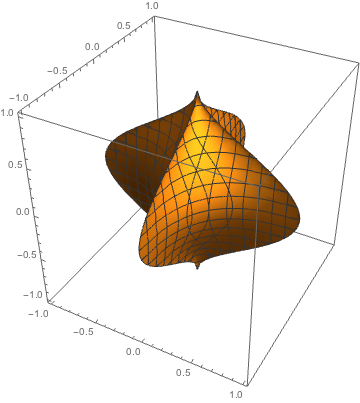
And here's the code:

DynamicModule[{cols},
 cols = RGBColor /@ {"#F40968", "#FDEA2E", "#512E5E"};
 Manipulate[
  Show[Table[
    ParametricPlot3D[{{(1 - Abs[z]^(2) - Abs[y]^(1/2))^2, y, 
       z}, {-(1 - Abs[z]^(2) - Abs[y]^(1/2))^2, y, 
       z}}, {y, -(1 - Abs[z]^(2))^2, (1 - Abs[z]^(2))^2}, 
     PlotRange -> 1, Boxed -> False, Axes -> None, PlotPoints -> 200, 
     PlotStyle -> Blend[cols[[;; 2]], (z + 1)/2], 
     SphericalRegion -> False, ViewPoint -> 65 {1, 0, 1}, 
     ViewAngle -> ?/250, ImageSize -> 540, 
     Background -> cols[[3]]], {z, -1 + t, 1 - .001, 1/8}]], 
    {t, .001, 1/8}]]