You have a few typos but after those are corrected the fix is to have better starting values for the parameters (as the default starting values for both xc and m are 1.
data = {{0, 0}, {30, 18.186}, {60, 30.98166667}, {90, 39.843}, {120, 45.865}, {150, 51.274},
{180, 55.98333333}, {210, 60.13}, {240, 63.81933333}, {270, 67.398}, {300, 70.59},
{330, 73.8}, {360, 76.9}, {390, 79.5}, {420, 82}, {450, 85}, {480, 88.16}, {510, 91.68},
{540, 94.2}, {570, 95.73}, {600, 96.9}, {630, 99.042}, {660, 99.3}, {690, 99.7}, {720, 99.82},
{750, 100}, {780, 100}, {810, 100}, {840, 100}, {870, 100}};
nlm = NonlinearModelFit[data, 100 (1 - Exp[-Abs[x/xc]^m]), {{xc, 10}, m}, x];
nlm["BestFitParameters"]
(* {xc -> 213.862, m -> 0.951079} *)
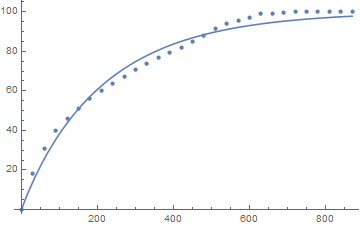
But the fit is not great:
Show[ListPlot[data],
Plot[nlm[x], {x, Min[data[[All, 1]]], Max[data[[All, 1]]]}]]