Because It's There
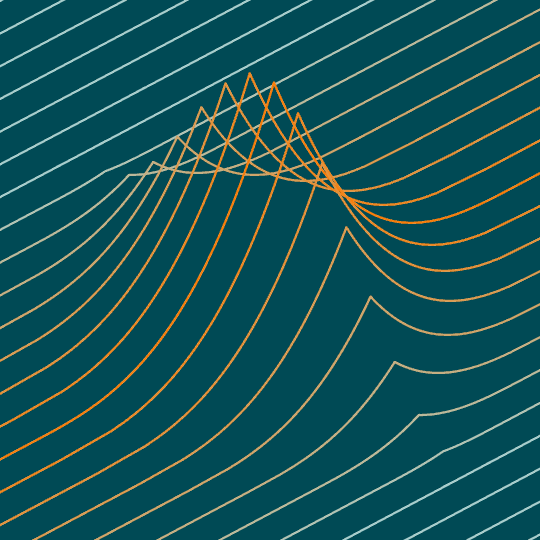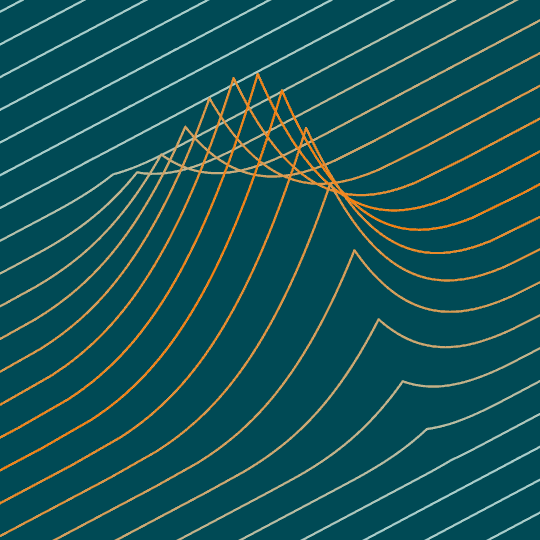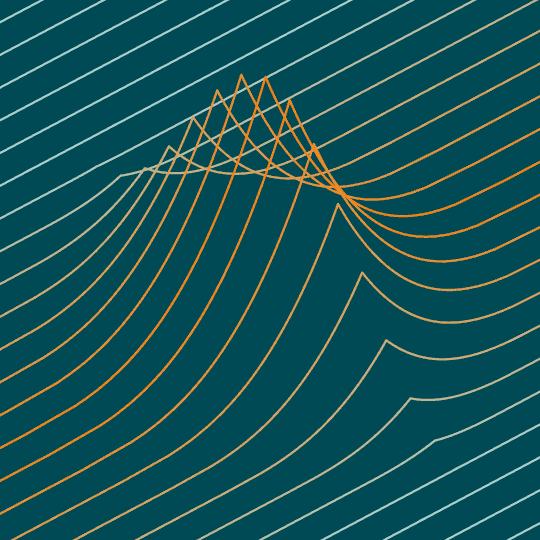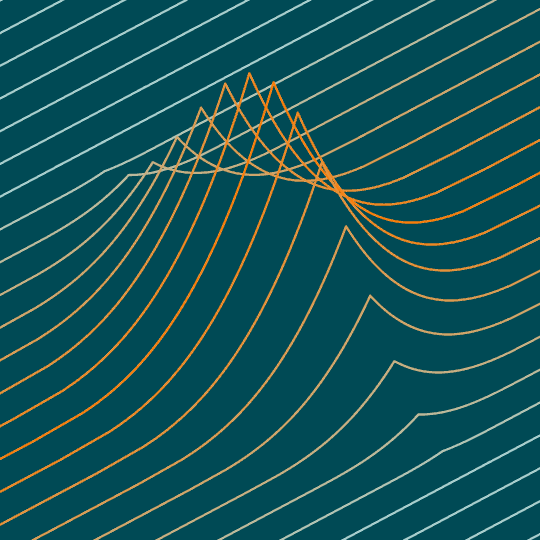
Same basic idea as Phoenix, this time with the top half of the surface $|x|+y^2+\sqrt[3]{z}=1$.
By the way, I'm now selling prints if you're interested in putting some of my work on your wall.
Here's the code:
DynamicModule[{cols},
cols = RGBColor /@ {"#A7CDCC", "#F87D09", "#A7CDCC", "#004A55"};
Manipulate[
Show[Table[{ParametricPlot3D[{{(1 - z^(1/3) - y^2), y,
z}, {-(1 - z^(1/3) - y^2), y, z}}, {z, 0,
Max[(1 - y^2)^3, .001]}, PlotRange -> 2, Boxed -> False,
Axes -> None, ViewPoint -> 65 {1.2, 1.5, 1.7},
ViewCenter -> {.504, .5, .55}, ViewAngle -> ?/1200.,
ImageSize -> 540,
PlotStyle ->
Directive[Blend[cols[[;; 3]], (y + 1)/2], Thickness[.004]],
Background -> cols[[4]]],
Graphics3D[{Thickness[.004], Blend[cols[[;; 3]], (y + 1)/2],
Line[{{# (1 - y^2), y, 0}, {2 #, y, 0}}] & /@ {-1,
1}}]}, {y, -2 + t, 2, 1/8}]], {t, 0, 1/8}]]