Group Abstract Group Abstract

Message Boards Message Boards

Solve this nonlinear delayed differential equation?

I am using NDSolve for the solution of the following delayed, dynamical nonlinear system

NLSol = NDSolve[{Derivative[1][cf][t] == -400. cf[t] + 
     124450.79348 Sin[100 \[Pi] t] - 
     400. Sign[-0.4 Cos[100 \[Pi] t] + TriangleWave[1000 t]] vdc[t], 
   Derivative[1][vdc][t] == 
    1000. cf[t] Sign[-0.4 Cos[100 \[Pi] t] + TriangleWave[1000 t]], 
   Derivative[1][a0][t] == 50 (cf[t] - cf[t - 1/50]), 
   cf[t /; t <= 0] == 0, vdc[t /; t <= 0] == 0, 
   a0[t /; t <= 0] == 0}, {cf[t], vdc[t], a0[t]}, {t, 0, 0.5}]

I am not sure what I am doing wrong to get the error "Input value {0.48} lies outside the range of data in the \ interpolating function " Please, help. Thanks in advance Jesus Rico
POSTED BY: J Jesus Rico-Melgoza
2 Replies
Sort By:

Marco, It is working as expected. Thank you very much! I guess some of us are very used to the idea that Mathematica would find the appropriate parameters for integration automatically. We have to be careful with that assumption.

Thanks again.

Jesus
POSTED BY: J Jesus Rico-Melgoza

Hi,

I haven't had much time to play around with it, but this seems to work ok-ish:

NLSol = NDSolve[{Derivative[1][cf][t] == -400. cf[t] + 124450.79348 Sin[100 \[Pi] t] - 400. Sign[-0.4 Cos[100 \[Pi] t] + TriangleWave[1000 t]] vdc[t], Derivative[1][vdc][t] == 1000. cf[t] Sign[-0.4 Cos[100 \[Pi] t] + TriangleWave[1000 t]], Derivative[1][a0][t] == 50 (cf[t] - cf[t - 1/50]), 
cf[t /; t <= 0] == 0, vdc[t /; t <= 0] == 0, a0[t /; t <= 0] == 0}, {cf[t], vdc[t], a0[t]}, {t, 0, 0.5}, Method -> {"DiscontinuityProcessing" -> False, 
"TimeIntegration" -> "Adams"}]

At least in the sense that it integrates over the entire interval. Then you can plot it:

Plot[{cf[t] /. NLSol[[1]], vdc[t] /. NLSol[[1]], a0[t] /. NLSol[[1]]}, {t, 0, 0.5}, PlotPoints -> 200, PlotStyle -> {Blue, Red, Green}]

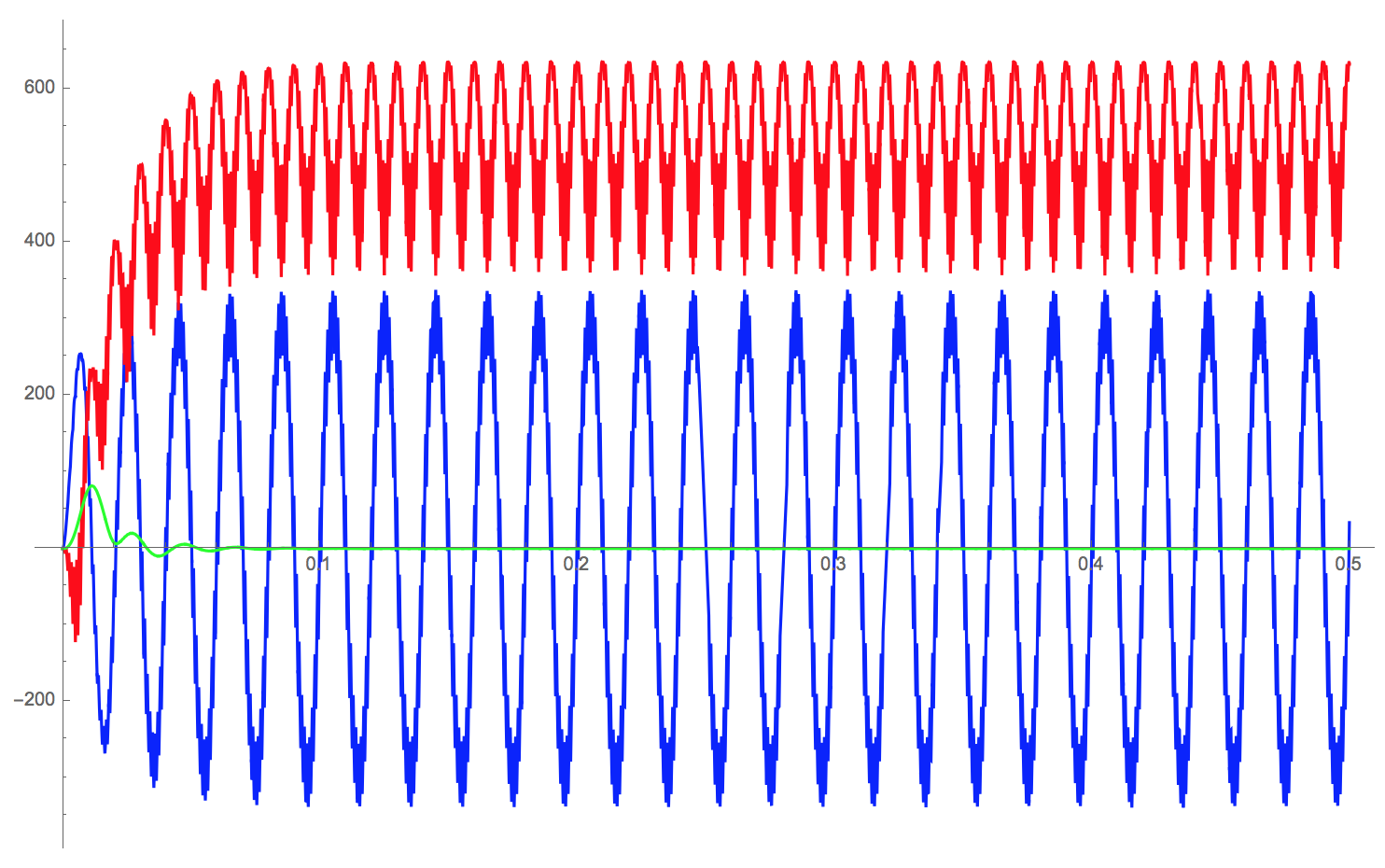
enter image description here

Cheers,

Marco
POSTED BY: Marco Thiel
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard