The problem is that ColorData["Pastel"] wants the argument between 0 and 1. You can rescale your curvature, though:

x = Sin[t] + 2/3 Sin[3 t];
y = Cos[t] + 2/3 Cos[3 t];
curvature[t_] =
  (D[x, t] D[y, {t, 2}] - 
     D[y, t] D[x, {t, 2}])/(D[x, t]^2 + D[y, t]^2)^(3/2);
ParametricPlot[{Sin[t] + 2/3 Sin[3 t], Cos[t] + 2/3 Cos[3 t]}, {t, 0, 
  2 Pi}, ColorFunction -> 
  Function[{x, y, u}, 
   ColorData["Pastel"][
    Rescale[curvature[u], {curvature[Pi/2], curvature[0]}, {0, 1}]]], 
 ColorFunctionScaling -> False]

Okay, so I've realized that what I'm trying to do is vary the Hue or shade of the curve by it's curvature.

ParametricPlot[{Sin[t] + 2/3 Sin[3 t], Cos[t] + 2/3 Cos[3 t]}, {t, 0, 2 Pi}]

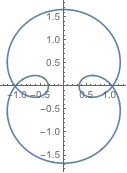
So the loops with more curvature would appear a different color than the flatter parts of the curve. No luck so far. I've tried:

x = Sin[t] + 2/3 Sin[3 t];
y = Cos[t] + 2/3 Cos[3 t];

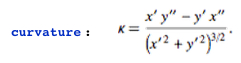
curvature = (D[x, t] D[y, {t, 2}] -D[y, t] D[x, {t, 2}])/(D[x, t]^2 + D[y, t]^2)^(3/2)


ParametricPlot[{Sin[t] + 2/3 Sin[3 t], Cos[t] + 2/3 Cos[3 t]}, {t, 0, 2 Pi}, 
ColorFunction -> Function[{x, y, t}, ColorData["Pastel"][curvature]]]

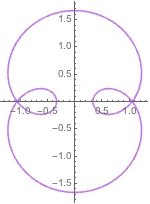
(Doesn't work). I've also tried

ColorFunction -> Function[{x, y, t}, Hue[curvature]]

to no avail. And I looked into ArcCurvature and FrenetSerretSystem but couldn't come up with a solution. Any ideas?

You need to use the 3rd argument in this case (go to the help of ColorFunction there it will be shown which parameters and in what order are passed on to ColorFunction. ParametricPlot in this case gets x,y,t values...

ParametricPlot[{Cos[4 t] - Cos[0.5 t] + Sin[t], Sin[3 t] - Sin[2 t]}, {t, 0, 4 Pi}, PlotStyle -> Thickness[0.01], ColorFunction -> Function[{x, y, t}, Hue[0.1 Sin[0.3 t] - Sin[2 t]]]]