Group Abstract Group Abstract

Message Boards Message Boards

Varying color parametrically along a curve?

Bryan Lettner
Posted 9 years ago
POSTED BY: Bryan Lettner
5 Replies
Sort By:

The problem is that ColorData["Pastel"] wants the argument between 0 and 1. You can rescale your curvature, though:

x = Sin[t] + 2/3 Sin[3 t];
y = Cos[t] + 2/3 Cos[3 t];
curvature[t_] =
  (D[x, t] D[y, {t, 2}] - 
     D[y, t] D[x, {t, 2}])/(D[x, t]^2 + D[y, t]^2)^(3/2);
ParametricPlot[{Sin[t] + 2/3 Sin[3 t], Cos[t] + 2/3 Cos[3 t]}, {t, 0, 
  2 Pi}, ColorFunction -> 
  Function[{x, y, u}, 
   ColorData["Pastel"][
    Rescale[curvature[u], {curvature[Pi/2], curvature[0]}, {0, 1}]]], 
 ColorFunctionScaling -> False]
POSTED BY: Gianluca Gorni
Bryan Lettner
Bryan Lettner
Posted 9 years ago

works great thank you!

enter image description here
POSTED BY: Bryan Lettner
Updating Name
Updating Name
Posted 1 year ago

Is there any way to show that curvature in bar legend?
POSTED BY: Updating Name
Bryan Lettner
Bryan Lettner
Posted 9 years ago

Okay, so I've realized that what I'm trying to do is vary the Hue or shade of the curve by it's curvature.

ParametricPlot[{Sin[t] + 2/3 Sin[3 t], Cos[t] + 2/3 Cos[3 t]}, {t, 0, 2 Pi}]

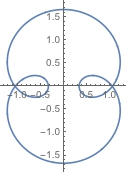
enter image description here

So the loops with more curvature would appear a different color than the flatter parts of the curve. No luck so far. I've tried:

x = Sin[t] + 2/3 Sin[3 t];
y = Cos[t] + 2/3 Cos[3 t];

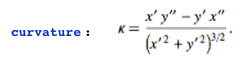
enter image description here

curvature = (D[x, t] D[y, {t, 2}] -D[y, t] D[x, {t, 2}])/(D[x, t]^2 + D[y, t]^2)^(3/2)


ParametricPlot[{Sin[t] + 2/3 Sin[3 t], Cos[t] + 2/3 Cos[3 t]}, {t, 0, 2 Pi}, 
ColorFunction -> Function[{x, y, t}, ColorData["Pastel"][curvature]]]

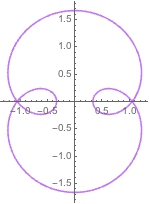
enter image description here

(Doesn't work). I've also tried

ColorFunction -> Function[{x, y, t}, Hue[curvature]]

to no avail. And I looked into ArcCurvature and FrenetSerretSystem but couldn't come up with a solution. Any ideas?
POSTED BY: Bryan Lettner

You need to use the 3rd argument in this case (go to the help of ColorFunction there it will be shown which parameters and in what order are passed on to ColorFunction. ParametricPlot in this case gets x,y,t values...

ParametricPlot[{Cos[4 t] - Cos[0.5 t] + Sin[t], Sin[3 t] - Sin[2 t]}, {t, 0, 4 Pi}, PlotStyle -> Thickness[0.01], ColorFunction -> Function[{x, y, t}, Hue[0.1 Sin[0.3 t] - Sin[2 t]]]]
POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard