Numerically you could write a function something like:
ClearAll[InverseGamma]
InverseGamma[x_?NumericQ]:=Module[{start,y},
If[Head[x]=!=Complex,
If[x>0.88561,
start=(-1+2 Log[x]-Log[2 \[Pi]])/(2 ProductLog[(-1+2 Log[x]-Log[2 \[Pi]])/(2 E)])+1-1/4;
Chop[y/.FindRoot[Gamma[y]==x,{y,start}]]
,
Missing[]
,
Missing[]
]
,
Missing[]
]
]
Show[{ParametricPlot[{Gamma[x], x}, {x, 1, 4}, PlotStyle -> Red],Plot[InverseGamma[x], {x, 0.88, 5}]}]
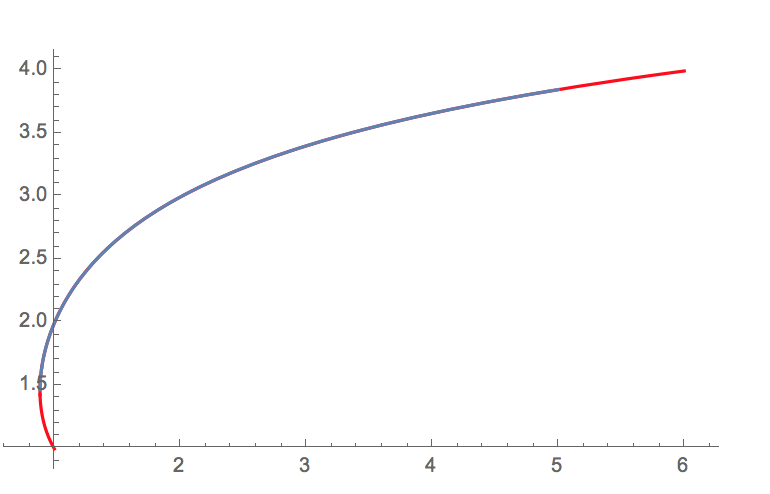
Of course this is not very fast but works reasonably for real numbers above 0.89. And good guess for the starting position of FindRoot helps a lot...