There isn't really anything I guess as it is multivalued as you can see...

--SH

thanks a lot. sometimes IGR doesn't match IG As you know. what should I do?

well, it IS invertible. But like x^2 => sqrt(x), you have to decide what to do for multiple values:

should it return +3 or -3? when one asks for x=9. Well this is by default +3 in Mathematica, you can imagine that this 'choice' becomes much more tricky with the Gamma function...

What should InverseGamma[4] return? You have to decide which one to return; I see like 6 possible values in your plot...

Numerically you could write a function something like:

ClearAll[InverseGamma]
InverseGamma[x_?NumericQ]:=Module[{start,y},
    If[Head[x]=!=Complex,
        If[x>0.88561,
            start=(-1+2 Log[x]-Log[2 \[Pi]])/(2 ProductLog[(-1+2 Log[x]-Log[2 \[Pi]])/(2 E)])+1-1/4;
            Chop[y/.FindRoot[Gamma[y]==x,{y,start}]]
        ,
            Missing[]
        ,
            Missing[]
        ]
    ,
        Missing[]
    ]
]


Show[{ParametricPlot[{Gamma[x], x}, {x, 1, 4}, PlotStyle -> Red],Plot[InverseGamma[x], {x, 0.88, 5}]}]

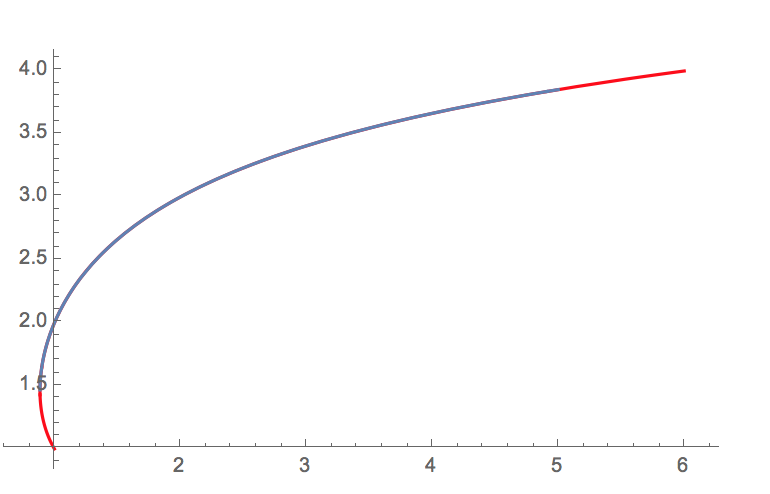
Of course this is not very fast but works reasonably for real numbers above 0.89. And good guess for the starting position of FindRoot helps a lot...

?(x) = digamma function = ?'/ ? , ?? = (positive zero of ?) - 1 , ??= ??!

If you want a Taylor series, you can just simply use:

Normal[InverseSeries[Series[Gamma[x], {x, 4.0, 10}]]]
Plot[%, {x, 1, 10}]

Where the expansion is around 4, with 10 terms.

I’m sorry to have troubled you . Please Kindly find the files attached. is it exact?

Attachments:

please help me

1. N
2. dn

Attachments:

Might we suggest the inverse of Stirling's Approximation? Assuming the isolation of the domain ( x ) of Stirling's Approximation for n! always has a fixed point x_k, for all independently chosen range values ( y ), this isolation is a function f(x) and if function f is composed infinitely for y is a member of the set of real numbers and x is a member of the set of real numbers, then the infinite composition is the inverse of Stirling's Approximation for n!