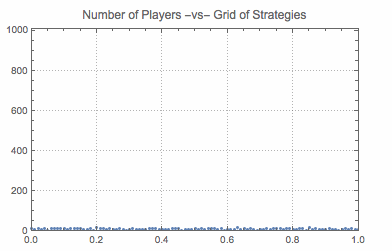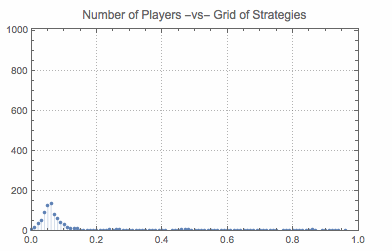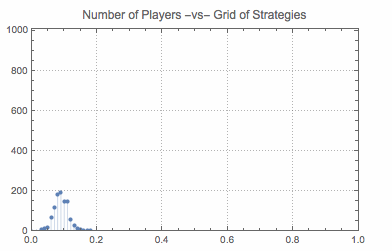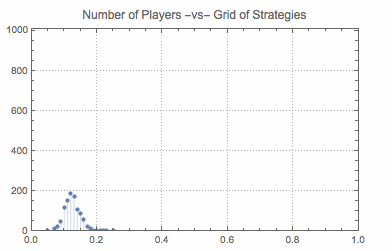
General information

The research is concerned with sampling dynamics (more precisely with 1-sampling dynamics). The idea was introduce in Osborne, M. J., & Rubinstein, A. (1998). Games with procedurally rational players. American Economic Review, 834-847. This procedure in dynamic setting leads to a Markov chain that can be approximated with a system of ordinary differential equations along the lines of Benaïm, M., & Weibull, J. W. (2003). Deterministic approximation of stochastic evolution in games. Econometrica, 71(3), 873-903. Approximation along these lines was first proposed in Sethi, R. (2000). Stability of equilibria in games with procedurally rational players. Games and Economic Behavior, 32(1), 85-104 (in an ad hoc manner). This is as far the procedure goes.

The game I am interested in is, so called, Ultimatum Bargaining game. There is an extensive literature on this game but the notebook is concerned with a variant proposed in Mi?kisz, J., & Ramsza, M. (2013). Sampling dynamics of a symmetric ultimatum game. Dynamic Games and Applications, 3(3), 374-386. The analysis offered in the last paper is concerned with a game with 3 strategies. The notebook explores (through simulations) what can happen with more strategies. What follows is (a) more precise description of a game and a step by step description of a Mathematica code.

The game

The standard ultimatum game is a two-player game. One player is called a proposer and the other is called a responder. The goal of the game is to divide a pie (of size 1 for simplicity) between the players. Proposer offers a share $\delta\in [0,1]$ and responder can either accept or reject the offer. If the offer is accepted, the proposer receives payoff $1-\delta$ and the responder gets the proposed offer, that is $\delta$.

The variant investigated in the following code is concerned with a symmetric version of this game. That is, each player can be either a proposer or a responder with equal probabilities. Thus, a strategy is a pair of numbers $(\alpha, \beta)$ both from the interval $[0,1]$. Parameter $\alpha$ is interpreted as an offer if a player is a proposer while parameter $\beta$ is interpreted as the minimal accepted offer if a player is a responder. For good reasons it is assumed that $\alpha=\beta$ and this value is further reffered to as $\delta$ (see Mi?kisz, J., & Ramsza, M. (2013). Sampling dynamics of a symmetric ultimatum game. Dynamic Games and Applications, 3(3), 374-386).

Code

The code starts with parameters of the simulation.

n = 3;
strategies = Table[k/n, {k, 0, n}];
numberOfStrategies = Length[strategies];
numberOfPlayers = 10000;
playerIndices = Range[1, numberOfPlayers];
tEnd = 200000;
population = RandomChoice[strategies, numberOfPlayers];

The main point here is that a population is just a list with randomly selected strategies (values of $\delta$). The next loop is the main loop of the simulation.

path = Reap@For[t = 1, t <= tEnd, t++,
    rp = First@RandomSample[playerIndices, 1];
    ro = RandomChoice[playerIndices, numberOfStrategies];
    roles = RandomChoice[{0, 1}, numberOfStrategies];
    payoffs = Table[0, {k, 1, numberOfStrategies}];
    For[k = 1, k <= numberOfStrategies, k++,
     If[roles[[k]] == 0 && strategies[[k]] >= population[[ro[[k]]]], 
      payoffs[[k]] = 1 - strategies[[k]]];
     If[roles[[k]] == 1 && strategies[[k]] <= population[[ro[[k]]]], 
      payoffs[[k]] = population[[ro[[k]]]]];
     ];
    pos = RandomChoice[Flatten@Position[payoffs, Max[payoffs]]]; 
    population[[rp]] = strategies[[pos]];
    Sow[Sort@Tally[population]];
    ];

So, first I select a random player (a random index). Next I select a list of random opponents (again random indices). Further a list of roles is selected with the interpretation that 0 is a proposer and 1 is a responder. The next loop is implements the following learning procedure. A randomly selected player, takes the first strategy and plays it against a strategy of a randomly selected opponent in a random role. This is repeated for all strategies and gives a list of payoffs associated with strategies. Next two lines select all best payoffs (positions of payoffs) and select at random one of those. The associated strategy is then adopted by the player randomly selected at the beginning. This process is repeated and induces behavior of population (what share of players uses what strategies).

In short, the procedure that governs evolution of population state is the following: random player runs a procedure to choose the best strategy given the state of population. This procedure is the following: play each strategy once (hence 1-sampling) and see what payoffs are received. Adopt the strategy that has yielded the best payoff (or select at random if there are many).

Notes

The above code can be made to be faster by doing the following: (a) using numerical values for strategies instead of symbolic values. (b) the inner For loop can be substituted with Table or other vectorized approach. The Sort@Tally takes a lot of time so instead the whole population can be Sown (resulting in a lot of memory for large populations). The outer loop cannot be (easily) replaced with vectorized approach and the simulation cannot be parallelized since the steps come in a sequence.

Attachments: