Recently I found out about Mondrian Art Puzzles, and decided to take a look. The idea is to divide a unit-sided square into differently sized unit-sided rectangles so that the area difference between the largest and smallest rectangles are minimized. One good first step is to find possible sets of rectangles. Here's code to do that.

size = 10;
bb =Table[#[[1]],{#[[2]]}]&/@Select[{Quiet[Times@@#[[1]]],Length[#]}&/@Table[Select[Union[Sort/@Transpose[{Divisors[n],Reverse@Divisors[n]}]],Last[#]<size+1&],{n,2,Ceiling[size^2/4]}],Last[#]>0&];
Grid[Take[{Last[#]-First[#],Length[#],#}&/@SortBy[Union[Select[Flatten[Table[Union[Select[With[{sub=Flatten[Take[bb,{a,b}]]},Subsets[sub,{Length[sub]-3,Length[sub]}]],Total@#==size^2&]], {a,1,Length[bb]-3},{b,a+3,Length[bb]}],2],Length[#]>0&]],Last[#]-First[#]&],15]]

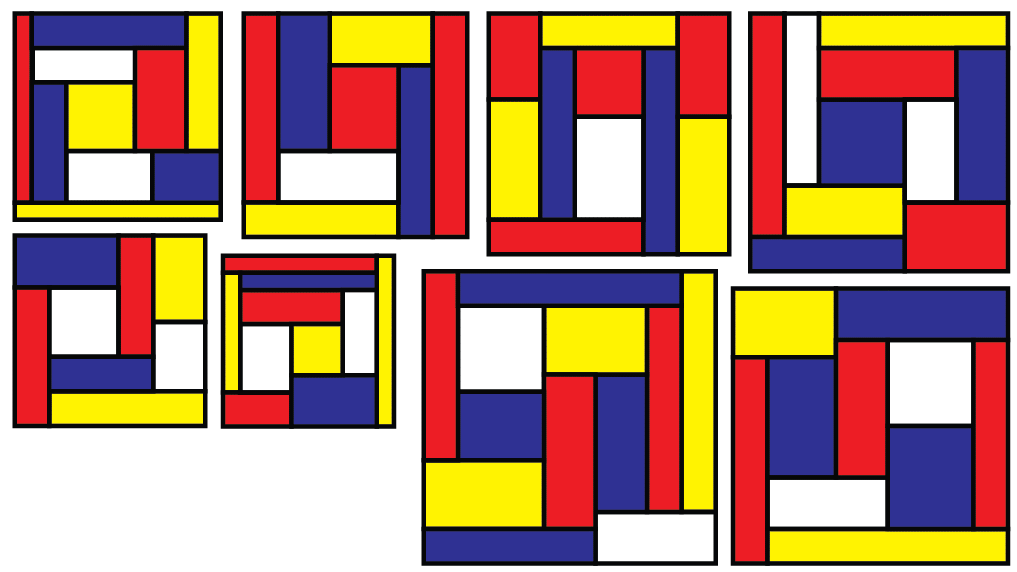
The next step is to find a tiling with those rectangles. I actually used Burr Tools for that step, but the techniques at the Easy Cube discussion might let Mathematica solve them. I beat the existing best solutions for everything above 10. Here's the best I found for 10x10 to 17x17.

Turn's out these were inspired by Blanche's Dissection -- Divide a square into 7 differently sized rectangles with the same area. I wondered if Mathematica could solve this problem.

Select[{a,b,c,d,e,f,g,h}/.RootReduce[Solve[
{e(b+c+d) == a(e+f) == g(a+b) == c(f+g) == b f == d(f+g+h) ==h(a+b+c),a+b+c+d==e+f+g+h==1}
]],Min[#]>0&][[1]]

{1/15 (8-Sqrt[19]),1/15 (1+Sqrt[19]),1/15 (-1+Sqrt[19]),1/15 (7-Sqrt[19]),
1/14 (7-Sqrt[19]),1/42 (-5+5 Sqrt[19]),5/21,1/21 (8-Sqrt[19])}

The code for that is easy! I couldn't find any dissections online for a 8-rectangle Blanche-type dissection of a square, so I pondered if Mathematica would work again.

sol =Select[{a,b,c,d,e,f,g,h,i}/.RootReduce[
Solve[{(a+b)(f+g)==(c+d+e)(f)==c g==d(g+ h)==(g+h+i)e==h (b+c)==(a)(i+h)==i(b+c+d),
a+b+c+d+e==f+g+h+i==1}]],Min[#]>0&][[1]];
xx = RootReduce[FoldList[Plus,0,Take[sol,5]]];
yy = RootReduce[FoldList[Plus,0,Drop[sol,5]]];
Graphics[{EdgeForm[Black],White,
Rectangle[{xx[[1]],yy[[1]]},{xx[[3]],yy[[3]]}],Rectangle[{xx[[3]],yy[[1]]},{xx[[6]],yy[[2]]}],Rectangle[{xx[[3]],yy[[2]]},{xx[[4]],yy[[3]]}],Rectangle[{xx[[4]],yy[[2]]},{xx[[5]],yy[[4]]}],Rectangle[{xx[[5]],yy[[2]]},{xx[[6]],yy[[5]]}],Rectangle[{xx[[2]],yy[[3]]},{xx[[4]],yy[[4]]}],Rectangle[{xx[[1]],yy[[3]]},{xx[[2]],yy[[5]]}],Rectangle[{xx[[2]],yy[[4]]},{xx[[5]],yy[[5]]}]}]

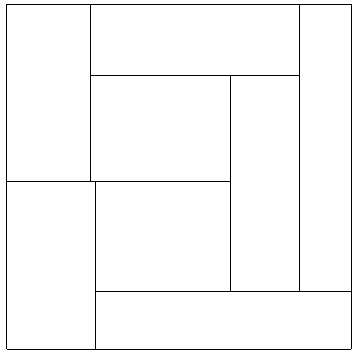
So yes, it works. Can we find a lot more? Can we find a dissection where all the side lengths are integers? Possibly. A network of rectangles that may lead to a solution is equivalent to a polyhedral graph. The original Blanche corresponds to the 5-wheel graph, and the new one here corresponds to Johnson 12. We have data on thousands of polyhedral graphs, so I just need to make some code that turns graphs into rectangle layouts.

To be continued....