The earth's gravitational field changes ever so slightly as we move on the earth, see also here. We can exaggerate the effect and plot a distorted "potato earth" to visualise this effect. The Wolfram Language's built in GeogravityModelData is perfect to produce 3d images like this one:

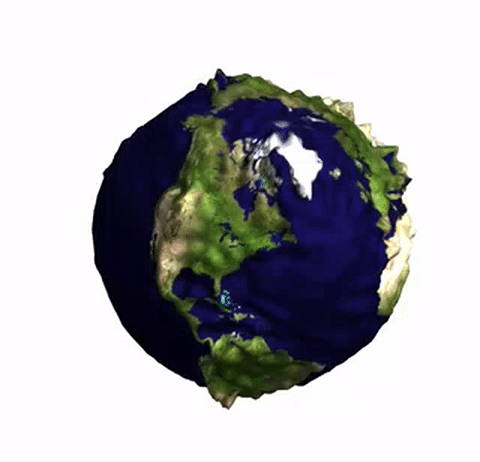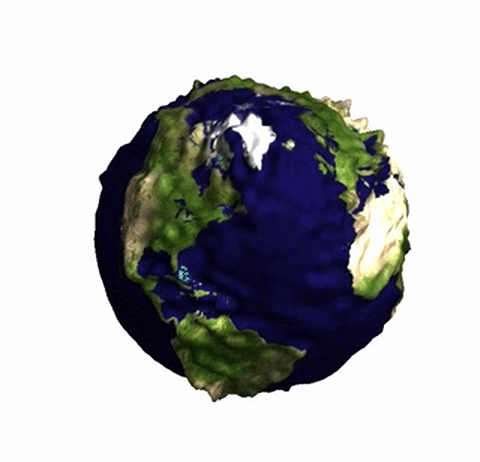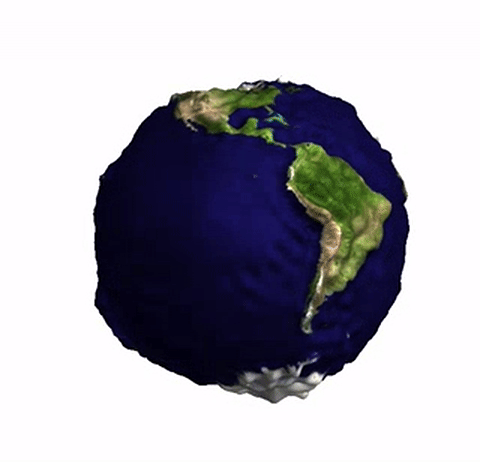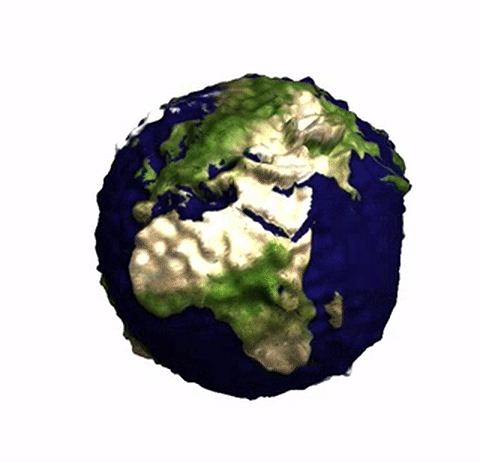
Generating this is actually quite trivial. We first load the built in data:

data = QuantityMagnitude@GeogravityModelData[{{-90, -180.}, {90, 180.}}, "Magnitude", GeoZoomLevel -> 0];
datamedium = Table[data[[k]]/Mean[data[[k]]], {k, 1, 128}];

You can play a bit with the GeoZoomLevel if you feel like it. We now have to translate this into changing radii of the globe. I therefore calculate deviations for averages over longitudes or alternatively latitudes to compare:

radius = 
 ListInterpolation[1. + 0.3 ((datamedium - Mean[Flatten@datamedium])/Differences[MinMax@datamedium][[1]]), {{0, Pi}, {0, 2 Pi}}, 
 InterpolationOrder -> 1]

or

radius2 = 
 ListInterpolation[1. + 0.3 Transpose@((Transpose@datamedium - Mean[Flatten@Transpose@datamedium])/
 Differences[MinMax@Transpose@datamedium][[1]]), {{0, Pi}, {0, 2 Pi}}, InterpolationOrder -> 1]

Note that I plot the gravitational strength at the surface as a change of the radius of the earth.

We can plot this on a 2D map; I do not like this particularly much, because I have the ugly fudge factor of 0.11 in the function, but it appears to work more or less.

ImageCompose[
ImageResize[ContourPlot[radius2[y, x], {x, 0 + 0.11, 2 Pi + 0.11}, {y, 0, Pi}, PlotRange -> All, Contours -> 75, ContourStyle -> None, 
ColorFunction -> "TemperatureMap", ImagePadding -> None, Frame -> False, AspectRatio -> 1/2], 1.04 ImageDimensions[worldmap]], {worldmap, 0.3}]

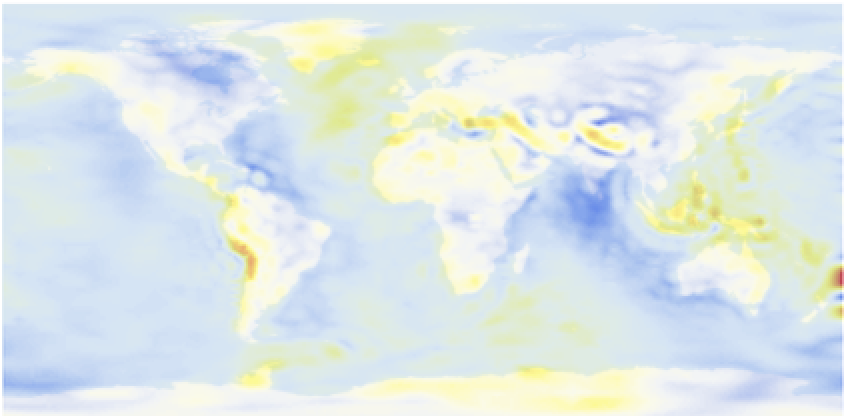
I will use a background image for the following plot, that is also in the documentation. I will attach it to this post. You might have to adjust the path to the image in the function.

SphericalPlot3D[radius[Pi - u, v], {u, 0, Pi}, {v, 0, 2 Pi}, TextureCoordinateFunction -> ({#5, 1 - #4} &), Mesh -> None, 
 PlotStyle -> Directive[Specularity[White, 10], Texture[Import["/Users/thiel/Desktop/backgroundimage.gif"]]], 
 Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip", Boxed -> False, PlotPoints -> 60]

For radius2 the function is trivially like this:

SphericalPlot3D[radius2[Pi - u, v], {u, 0, Pi}, {v, 0, 2 Pi}, TextureCoordinateFunction -> ({#5, 1 - #4} &), Mesh -> None, 
     PlotStyle -> Directive[Specularity[White, 10], Texture[Import["/Users/thiel/Desktop/backgroundimage.gif"]]], 
     Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip", Boxed -> False, PlotPoints -> 60]

This is, of course, quite trivial, but I liked the effect. I hope that I haven't made a mistake with the coordinates (it's late - 2:20am), but the 3d image looks good. There are strong peaks at the Rocky Mountains and the Andes, as well as the Himalayas.

Of course this applies to other data, too. If you want to try the magnetic field, this might work:

datamag = QuantityMagnitude@GeomagneticModelData[{{-90, -180.}, {90, 180.}}, "Magnitude", GeoZoomLevel -> 0];
datamediummag = Table[datamag[[k]]/Mean[datamag[[k]]], {k, 1, 128}];
radiusmag = ListInterpolation[1. + 0.3 ((datamediummag - Mean[Flatten@datamediummag])/Differences[MinMax@datamediummag][[1]]), {{0, Pi}, {0, 2 Pi}}, InterpolationOrder -> 1];
SphericalPlot3D[radiusmag[Pi - u, v], {u, 0, Pi}, {v, 0, 2 Pi}, TextureCoordinateFunction -> ({#5, 1 - #4} &), Mesh -> None, 
PlotStyle -> Directive[Specularity[White, 10], Texture[Import["/Users/thiel/Desktop/backgroundimage.gif"]]], Lighting -> "Neutral", Axes -> False, RotationAction -> "Clip", Boxed -> False, PlotPoints -> 60]

You will see that the surface is much smoother. This one really looks like a potato earth...

Cheers,

M.

Attachments: