Inspiration and Idea
The prospect of internalizing some notion of pure mathematics into the Wolfram Language has been talked about at various points in the past, such as in this post. My background is in proof assistants and type theories, and I've spent several years programming in languages like Agda and Coq. These dependently typed languages have the best track record for expressing formal mathematics, but the Wolfram Language can't be easily modified to replicate the behaviour of such languages. The issue, as I've come to understand it now, is that the rule-replacement computational model that the Wolfram Language uses is, at it's core, incompatible with a system-wide type theory. That is to say, such a system cannot have every term be typable while maintaining usability. So, what are the alternatives?
As far as I can tell, there are two major branches of dependently typed languages (and several minor ones), the "formal" type theories, such as Agda, Coq, Lean, Idris, etc., and the "semantic" type theories, being NuPRL and the more recent RedPRL. I started learning about that second branch a few months ago. Unfortunately, all current PRL implementations are largely unusable for an ordinary user, but the ideas underlying their approach to type theory was enamoring to me. The approach is as follows;
- Start with an untyped computational model (any will do).
- Use a programming logic to declare some forms from the model to be "canonical types".
- Declare other forms from the model to be "canonical terms" of the already declared type.
- Declare equations which define computational behaviors for those symbols intended to interact with the type under consideration.
As an example, it's typical to start with an untyped lambda calculus + constants as a computational model. If we want to define the booleans, we first must choose a symbol and declare it to be a canonical type. We would use an already existing term, in this case we can use the constant "bool", and state something like;
DeclareType bool
Which adds a rule to our environment allowing us to prove that bool is a type. Similarly, we would declare the two terms in the boolean type;
DeclareTerm True bool
DeclareTerm False bool
As before, the forms "True" and "False" existed in the language already, we are simply adding user-defined rules which allow us to reason about them as terms of a type.
The last step is to declare the defining computational behaviour for the type. This basically involves declaring the constant ABT "if(a. A, b, T, F)" to follow particular sequent rules, being;
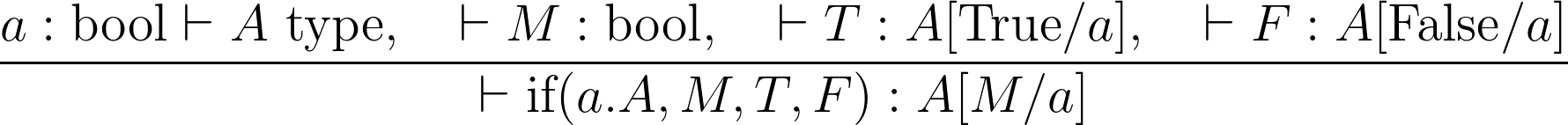
Actual programming syntax can vary on this, but with the Wolfram Language's Notation Package, I can make the declarations within the system I'll describe in this post match fairly closely to the sequent calculus syntax.
PRL languages expand on this idea by saying that one must define a series of partial equivalence relations (PERs) for each type. I take this approach in the third part of this post.
After studying this kind of system for a few weeks, Mathematica 11 hit, and I had an epiphany. This approach is 100% compatible with the Wolfram Language, and I decided to try implementing something like this. After about 2 weeks, I feel that I've had quite a bit of success, and I figured my project could benefit from some input from others.
A Very Basic Proof Assistant
Rules for Reasoning
To start out, I want to implement the sequent calculus in such a way that it's user friendly to prove basic statements. This first example will be a simple implementation of a proof assistant for (Hilbert-style) propositional logic. Starting out, I can declare the encoding I want to use to have special notations using the Notation package.
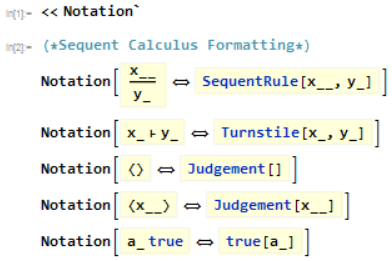
Using this, I can express rules like modus ponens as;
SequentRule[
Turnstile[Judgement[], Judgement[true[Implies[A, B]]]],
Turnstile[Judgement[], Judgement[true[A]]],
Turnstile[Judgement[], Judgement[true[B]]]]
And have it display as;

Thus mimicking a sequent. I'll expand on this when I get to implementing an actual type system
The idea I have is to first state a goal, then treat this sort of rule as a pattern. You start with a pattern like;
B true
And then apply modus ponens to get the goals
A => B true
A true
If the original goal is a theorem in our logic, then applying existing rules in the correct order will discharge all goals. Before such a system can be made, we need to process our rules into replacement rules that can actually be applied. This involves sugaring the hypotheses with context variables and turning the appropriate variables into patterns.
If we were to declare modus ponens as;

We want to get a rule out (which will be stored as ReversePattern[ModusPonens]) which we can apply to a goal. At the end of the processing our rule looks like;
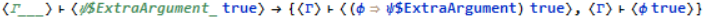
The $ExtraArgument part is added to avoid problems with variable capture during user interaction (maybe it would be a good idea to do this to the context variable as well, but for now it's fine). Notice that the phi is not turned into a pattern or altered in any way. The processing algorithm notices that phi appears in the antecedent goals, but not the conclusion. This means the user has to tell the system what phi is supposed to be since there's no other way to get it. All the variables required by the user are stored in the list ExtraArguments[ModusPonens]. The newly declared rule is then added to a list of known rules. After implementing this, we can declare all the rules we want;

Notice the DeclareSymbol command at the top. This just adds the symbols to a list called DeclaredSymbols which by default contains symbols such as true, Judgement, SequentRule, Turnstile, etc. By adding symbols to this list, they won't be turned into patterns by the processor. Additionally, we want to verify the behaviour of algorithms which may try to evaluate when we don't want them to during proof construction. Since I'm using the built-in Implies and Not, they will try to evaluate on certain arguments. For example "A => A" evaluates to "True", but I want to prove that as a theorem from the axioms. To prevent this, symbols with computational behaviour have to be rendered Inactive. I'll talk about reactivating them near the end of this section.
You may also notice the ImplicationFormer and NegationFormer rules. In a proper formalization of classical (and many other) logics, the axiom rules should have extra hypotheses which require one to prove that a particular variable is a well-formed formula/proposition. I decided not to use them for this post, but they should be used in a serious development.
User Interaction
I designed a simple interface for picking and applying declared rules. I'll probably put it into a window at some point, but for now it looks like this;
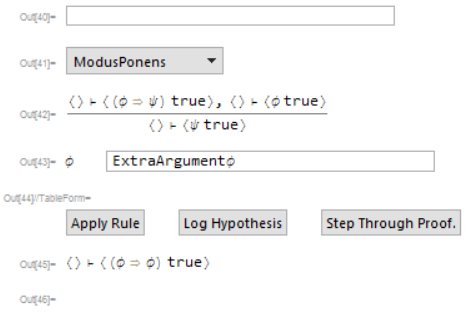
The top two components are a drop-down menu showing all available rules, and an input field for filtering the drop-down menu. The second two are a preview of what the declared rule looks like, and an auto-generated list of input fields for arguments required for completely applying a rule. The apply rule button applies the selected rule, and I'll explain the other two buttons in a bit. At the bottom is the current goal (in this case, I want to prove that A implies A), and below that is a (currently blank) string of text for storing error messages. Here's a gif of me proving the goal;
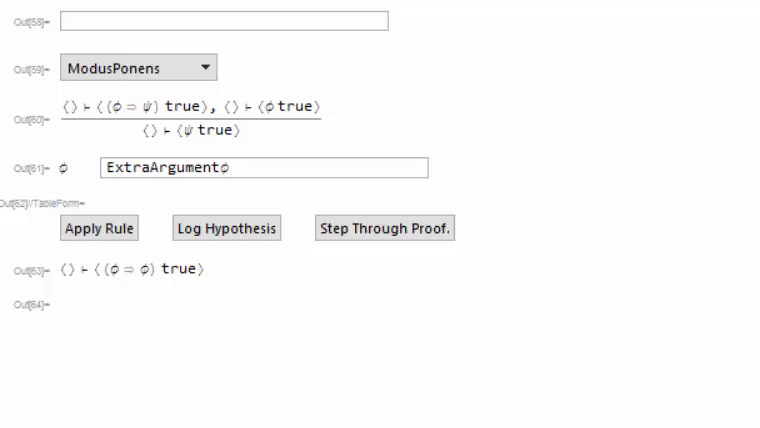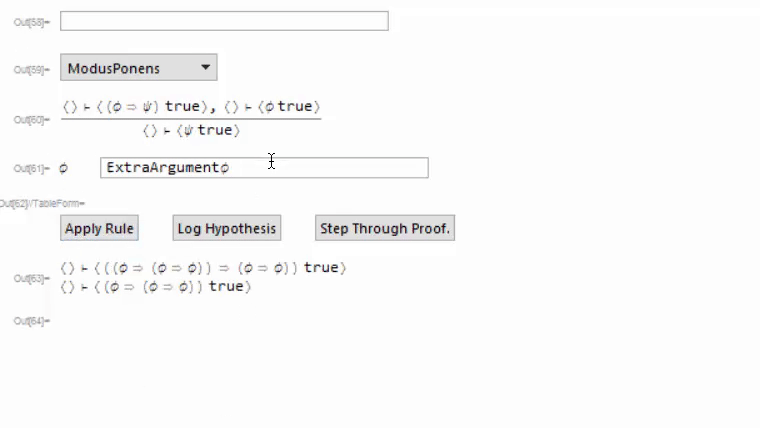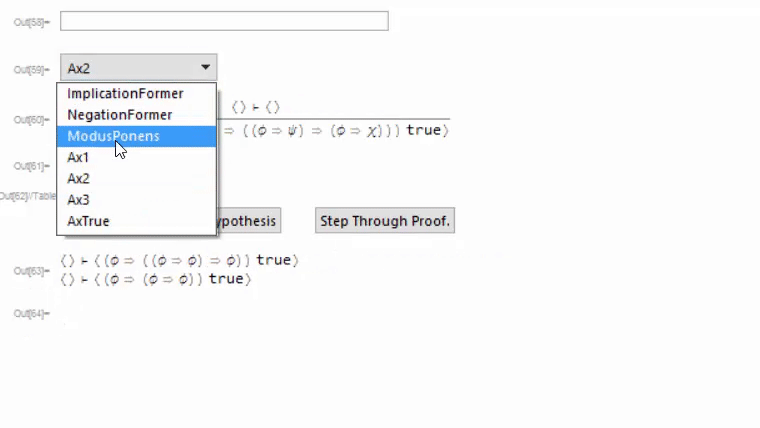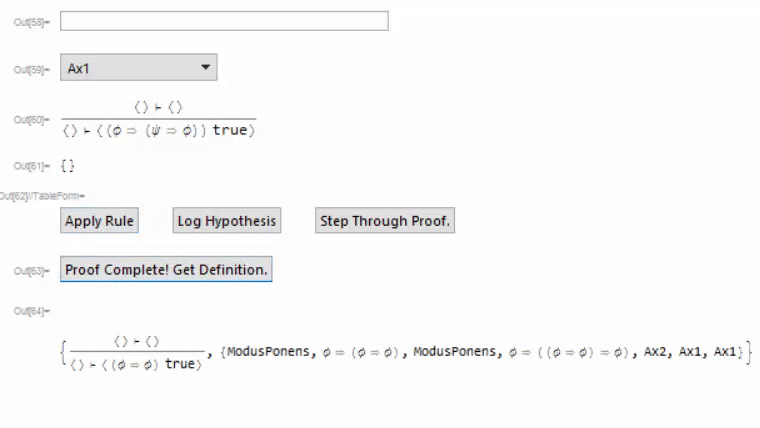
At the end we can get the proof we made and the rule which we proved. After the fact, we can check that this proof is correct by issuing it to CheckProof[provedRule, proof], which will return True if the proof is valid. It works by applying the rules in the proof in the same way they were applied when the proof was originally constructed, then checking if all goals have been discharged.
Additionally, we can add proven rules to the environment via an AddTheorem command that adds a rule the same way that DeclareSequentRule does, but only if the proof correctly checks.
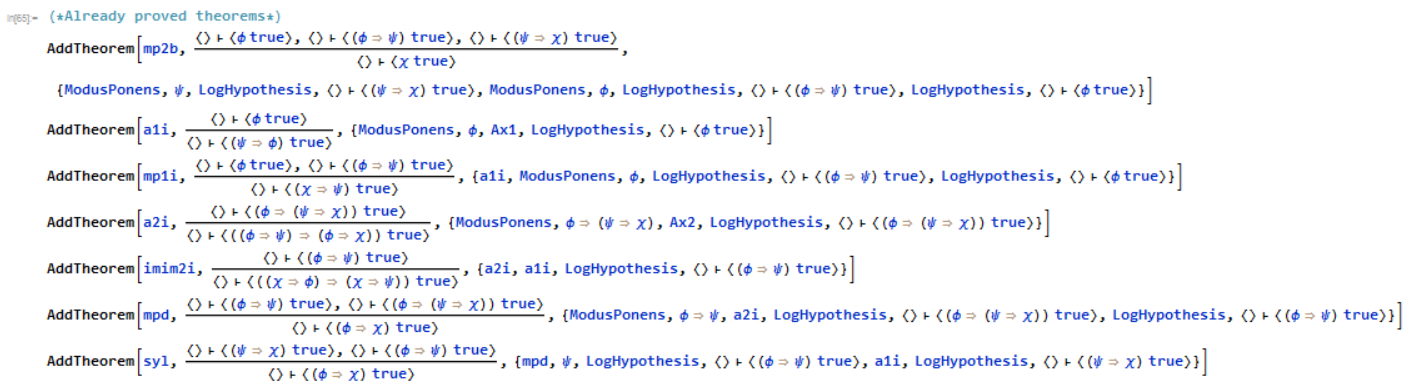
You'll notice that all the theorems with non-empty antecedents have "LogHypothesis" in their proofs. This is added when the "Log Hypothesis" button is pressed in the UI. By deriving the hypothesis from the target and logging it, it will remove the hypothesis from the goal and add it to the rule being proved.
Calling The System
You may be asking yourself, "hey, can't we already use Simplify to test when a proposition is true? If I were proving things in a more sophisticated logic that relies on classical propositional logic (Say, ZFC) it would be useful to actually utilize the built in capabilities of the Wolfram Language. We can manually add a rule that makes a call to the simplifier;

Using this we may have a complicated goal like;
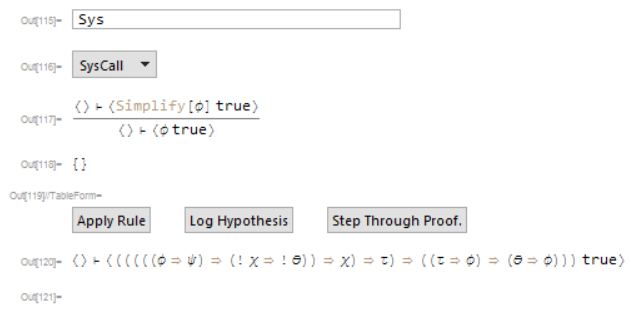
and issue a system call to immediately get;
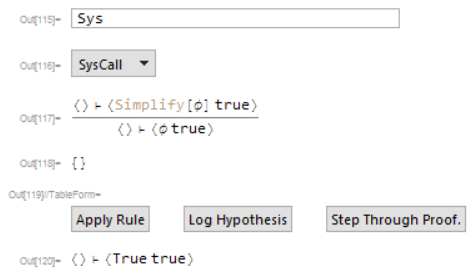
Which is trivially provable. Later in this post, I make use of similar rules to interface a type system with the already existing language.
Tactics
I've not invested very much time thinking about tactics, but the system as it stands can be extended with them. I added one called "BranchSearchTactic" which does a breadth-first search over all rules that don't require user interaction. If it finds a proof, it will add it to the currently building proof and discharge the goal. Here is a usage example;
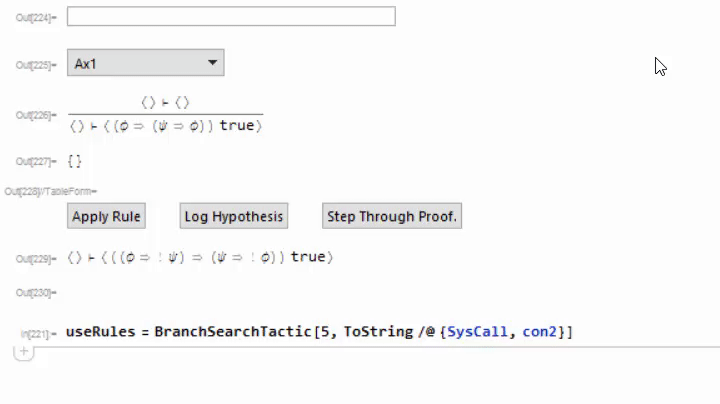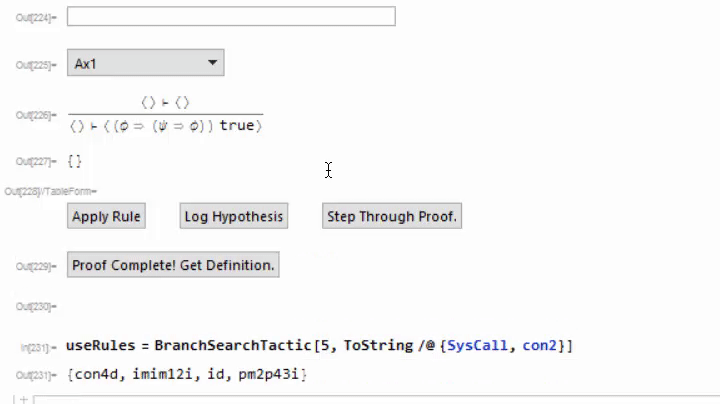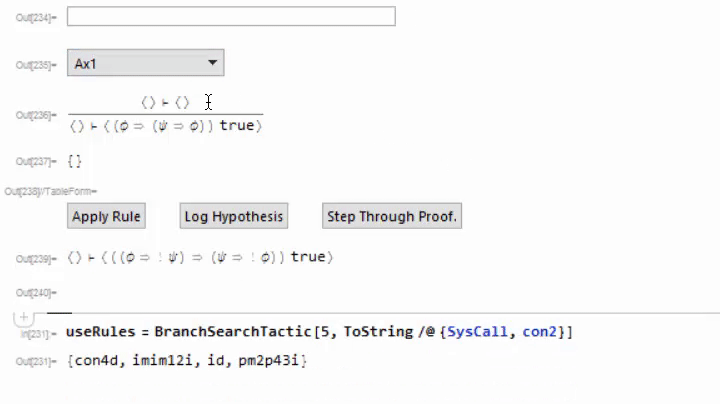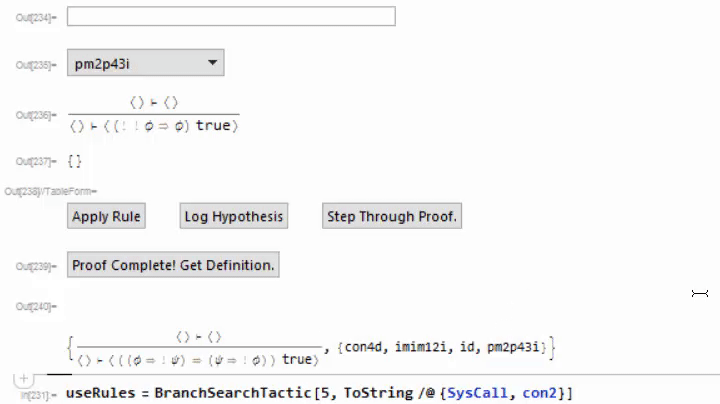
This is a useful tactic for proving that some term is well-formed. I use this frequently when constructing proofs in the type system. Future work should include an expanded library of tactics.
Implementing Types and Formally Verifying Programs
Rules for a Simple Dependent Type Theory
The rules for an actual type theory are similar to what you'd see for any logic, but they are far more complicated than propositional logic. I will take the approach of implementing type theory using PERs for defining type behaviors. Before this can be done, I first add rules for manipulating equations;


Several of those rules are redundant or maybe undesirable, but I include them here as examples.
The most typical type for a dependently typed language is the pi-type, who's typing rules can be declared in the style that you'd see in a technical paper on type theory.

The vertical tildes mark variable bindings, representing those bindings created by the abstract binding tree we're defining. The Wolfram Language doesn't properly handle variable binding (you can't test for alpha-equivalence, for example), but we don't need it to for the examples I make in this post.
Notice the presence of substitutions in the inference rules. We now are working with rules who's form may be determined by an intra-rule substitution. A straightforward pattern and replace application would fail to correctly apply the given rules. As a result, we must get the pre-substitution information from the user. After that, these arguments are substituted into the pattern, then the in-pattern substitutions must be performed. This will get us a working replacement rule. Other rules, such as the typing rule for if, also have a substitution in the antecedents. This must also be performed in order to get the correct post-application goal to the user.
Using the declared rules we can formally verify some basic programs, such as the S combinator;
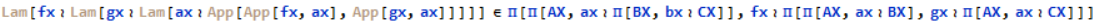

You'll notice that we had to do this by hand. Type checking has to be done by hand since it isn't decidable. This is because an arbitrary term does not have a unique type. In the future, it will probably be worth adding a tactic which can type-check a significant subset of the logic, even if it's technically impossible to check everything.
Sigma, Bool, and Coproduct Types
At this stage we can add in any of the standard types we want. For example, we can add sigma types, booleans, and coproducts like so;



This is sufficient for specifying more interesting theorems. For example, we can prove that all booleans are either True or False;
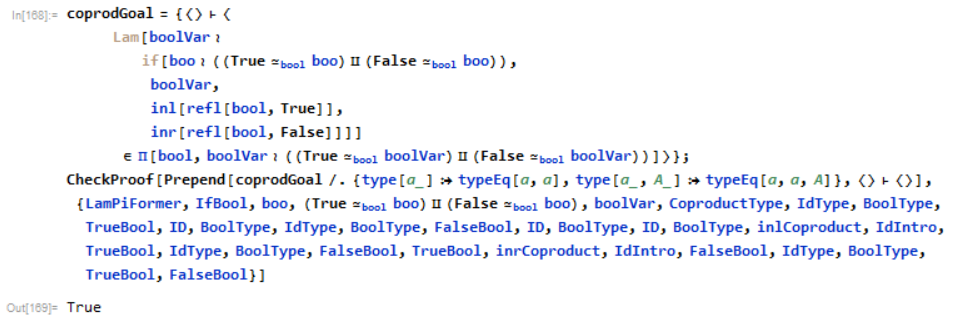
The Natural Numbers and Formal Verification
As a final example, we can define the type of natural numbers, along with it's dependent eliminator which represents mathematical induction.
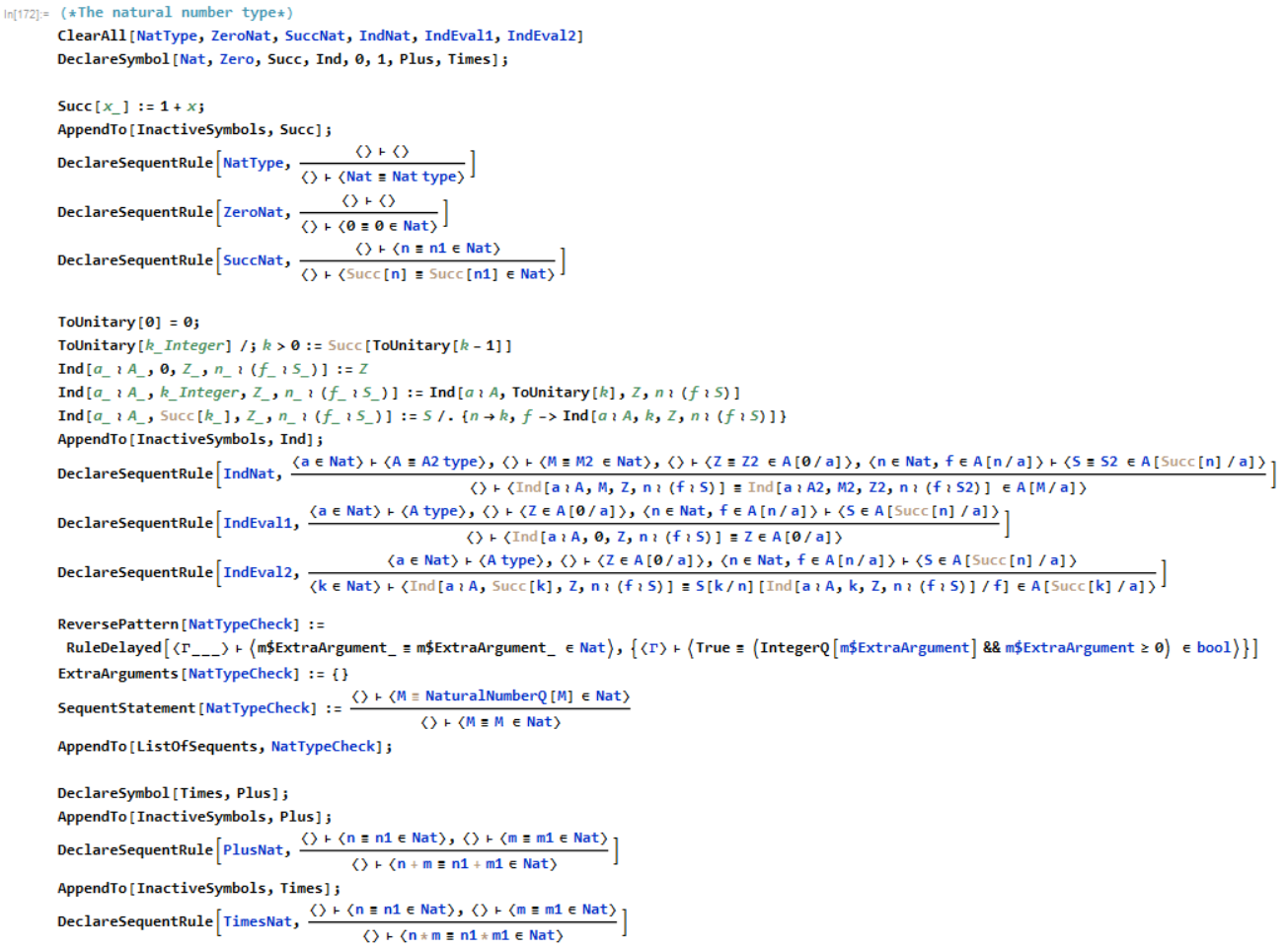
I had to do a bit of extra work to make it interface well with the built in representation of numbers. Also note that I declared Plus and Times in the type system. While both could have been defined in terms of induction, I would like to get the various built-in Wolfram Language functions to have their own typing rules so that the already existing system can interface with proofs. This way, we can make calls to the system using some custom rules;

These simply call Simplify on one or both arguments of an equation, but they can easily be modified to call other rule should we want to.
As a usage example, I want to prove that all numbers are either even or odd, that, for all natural numbers n, there exists a number z such that n = 2 * z or n = 1 + 2 * z. This is a simple proof by mathematical induction + a bit of algebra. Our initial goal looks like.

The term makes various references to "sys", which basically says "justify the equation in any way", which will be some calls to simplify in this case. For example, at some point in the proof we have the goal;

which asks us to prove Succ[n3] = Succ[2 * fst[f]] given a proof that n3 = 2 * fst[f]. One way we can approach this is to call SysCallEQ, simplifying both sides algebraically, which will reduce the equation to;
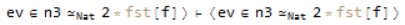
which is just our assumption. Later on in the same proof we encounter a different goal;
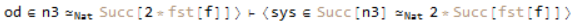
We may consider making the same system call as before. If we do this, we get to;
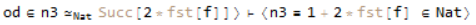
Which, unlike last time, is not one of our assumptions. We can then use transitivity to get us;

The first of those goals is trivially provable as our assumption. That second goal can be approached by calling Simplify on the left-hand side, getting us;
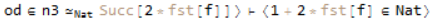
Which is easy to justify. While these are simple use cases, they suggest a greater potential for interfacing proofs with the already existing system.
In the end, the verification of the proof that all numbers are even or odd is around 500 steps. The point is to formally verify an algorithm, one which, given a number n, finds a z such that z is half of n (in the case of "inl") or z is half of n-1 (in the case of "inr"). Can this algorithm actually be run?

Yes, yes it can.
Future Work
Potential Generalizations
One system I implemented during testing was MU.

You'll notice that I had to put in the rules manually since the kind of pattern matching they use is incompatible with the processing done by DeclareSequentRule. It was this exercise which made me realize that the user interface was largely a way to systematically apply Replace on specific rules. The main thing preventing this from being strictly true is the handling of intra-rule substitutions. This suggests to me a potential generalization and even simplification of the system I've set out here. Early on, I noticed that my development was somewhat similar to Metamath, a small theorem prover. It may be prudent to borrow some of its methodology when modifying this system in the future.
Program Extraction
In theory, it should be possible to start with the type without any term as a goal, and interact with the user to build up a term which witnesses the type. I've had some small success in making a system which works like this, though it isn't nice enough to talk about in detail. This sort of feature is what makes dependently typed languages useful and usable in the first place. For now, my system can only verify a program, but building up a program from a specification will have to be a future project.
Libraries
I mentioned that I wanted to add typing rules (and theorems) for a large number of the Wolfram Languages' built in functions. There are many existing mature libraries for fields like graph and group theory for languages such as Coq and Agda. Making a similar library with compatibility with the already existing faculties for calculation and manipulation would be nice.
Extensions
There are many cutting-edge logics and type theories which are difficult to implement inside modern proof assistants. I think a system like the one I laid out here could be helpful for quickly setting up all the rules required to play with more speculative type theories, such as Adjoint Logic, Cubical Realizability, and Directed HoTT. In the future, I plan on trying to implement some of those myself.
 Attachments:
Attachments: