A solution without Table[]:

ListLinePlot[IntegerDigits[Range[100]^2][[All, 1]]]

From each row, select the first element.

Scroll down all the way in the left pane, past the last chapter and there is a link to all the solutions.

I wonder how many people gave up on EIWL because they couldn't solve the problems and didn't see the solutions buried at the bottom(off screen).

About Exercise 6.8:

Make a list line plot of the number of digits in each of the first 100 squares.

One of the possible solutions:

ListLinePlot[Table[Length[IntegerDigits[i^2]], {i, 1, 100}]]

Another solution:

ListLinePlot[
 Table[Length[IntegerDigits[Range[100]^2][[i]]], {i, 100}]]

Hi D.P.,

I'm working through the EIWL exercises myself, and am currently at Chp. 9. I remember this problem and came up with this solution, also using only the functions we've been taught so far in the book:

ListLinePlot[Table[First[IntegerDigits[n^2]], {n, 100}]]

The tasks defined in the exercises range from being enormously simple to just maddening, but I keep telling myself that this is just how it will be once I know enough to start applying the WL to real problems. And I've accepted that the repetition (yet another problem built around Table and IntegerDigits?) is all for the best.

By the way, I don't know if you're working off the web page or the MMA notebooks of EIWL, but I just found out that the downloadable MMA notebooks come with additional exercises in each chapter and also give you a way to enter and check your output (note: not your solution) against the expected answer directly in a notebook. This rather belated discovery has made working through EIWL much more enjoyable (even, yes, fun!).

ListLinePlot@Table[IntegerDigits[i^2][[1]], {i, 100}]

There are a lot of approaches to solve Problem 6.10

Make a list line plot of the first digits of the first 100 squares.

But, we must use only the functions exposed in the first 6 chapters. So...

We can generate a list of the first 100 squares:

In[1]:= Table[i^2, {i, 100}]

Out[1]= {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, \
225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, \
841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, \
1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, 2601, \
2704, 2809, 2916, 3025, 3136, 3249, 3364, 3481, 3600, 3721, 3844, \
3969, 4096, 4225, 4356, 4489, 4624, 4761, 4900, 5041, 5184, 5329, \
5476, 5625, 5776, 5929, 6084, 6241, 6400, 6561, 6724, 6889, 7056, \
7225, 7396, 7569, 7744, 7921, 8100, 8281, 8464, 8649, 8836, 9025, \
9216, 9409, 9604, 9801, 10000}

In this list, we must find the digits of each number:

In[39]:= IntegerDigits@Table[i^2, {i, 100}]

Out[39]= {{1}, {4}, {9}, {1, 6}, {2, 5}, {3, 6}, {4, 9}, {6, 4}, {8, 
  1}, {1, 0, 0}, {1, 2, 1}, {1, 4, 4}, {1, 6, 9}, {1, 9, 6}, {2, 2, 
  5}, {2, 5, 6}, {2, 8, 9}, {3, 2, 4}, {3, 6, 1}, {4, 0, 0}, {4, 4, 
  1}, {4, 8, 4}, {5, 2, 9}, {5, 7, 6}, {6, 2, 5}, {6, 7, 6}, {7, 2, 
  9}, {7, 8, 4}, {8, 4, 1}, {9, 0, 0}, {9, 6, 1}, {1, 0, 2, 4}, {1, 0,
   8, 9}, {1, 1, 5, 6}, {1, 2, 2, 5}, {1, 2, 9, 6}, {1, 3, 6, 9}, {1, 
  4, 4, 4}, {1, 5, 2, 1}, {1, 6, 0, 0}, {1, 6, 8, 1}, {1, 7, 6, 
  4}, {1, 8, 4, 9}, {1, 9, 3, 6}, {2, 0, 2, 5}, {2, 1, 1, 6}, {2, 2, 
  0, 9}, {2, 3, 0, 4}, {2, 4, 0, 1}, {2, 5, 0, 0}, {2, 6, 0, 1}, {2, 
  7, 0, 4}, {2, 8, 0, 9}, {2, 9, 1, 6}, {3, 0, 2, 5}, {3, 1, 3, 
  6}, {3, 2, 4, 9}, {3, 3, 6, 4}, {3, 4, 8, 1}, {3, 6, 0, 0}, {3, 7, 
  2, 1}, {3, 8, 4, 4}, {3, 9, 6, 9}, {4, 0, 9, 6}, {4, 2, 2, 5}, {4, 
  3, 5, 6}, {4, 4, 8, 9}, {4, 6, 2, 4}, {4, 7, 6, 1}, {4, 9, 0, 
  0}, {5, 0, 4, 1}, {5, 1, 8, 4}, {5, 3, 2, 9}, {5, 4, 7, 6}, {5, 6, 
  2, 5}, {5, 7, 7, 6}, {5, 9, 2, 9}, {6, 0, 8, 4}, {6, 2, 4, 1}, {6, 
  4, 0, 0}, {6, 5, 6, 1}, {6, 7, 2, 4}, {6, 8, 8, 9}, {7, 0, 5, 
  6}, {7, 2, 2, 5}, {7, 3, 9, 6}, {7, 5, 6, 9}, {7, 7, 4, 4}, {7, 9, 
  2, 1}, {8, 1, 0, 0}, {8, 2, 8, 1}, {8, 4, 6, 4}, {8, 6, 4, 9}, {8, 
  8, 3, 6}, {9, 0, 2, 5}, {9, 2, 1, 6}, {9, 4, 0, 9}, {9, 6, 0, 
  4}, {9, 8, 0, 1}, {1, 0, 0, 0, 0}}

We can generate a list of the first digits in each sub-list by different means. But, the beginner knows at this point only a few possibilities. First, we must identify every sub-list and its first element. For this, we use functions Part[] and First[]. Second, to generate a list, we use function Table[]:

In[43]:= Table[
 First@Part[IntegerDigits@Table[i^2, {i, 100}], j], {j, 100}]

Out[43]= {1, 4, 9, 1, 2, 3, 4, 6, 8, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, \
4, 4, 5, 5, 6, 6, 7, 7, 8, 9, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, \
4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, \
8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 1}

And finally, we can use ListLinePlot[]:

ListLinePlot[
 Table[First@Part[IntegerDigits@Table[i^2, {i, 100}], j], {j, 100}]]

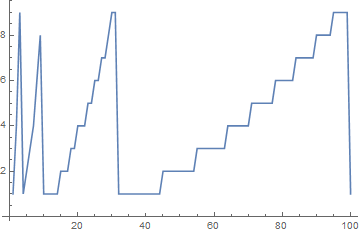
An equivalent code to the previous one:

ListLinePlot[
 Table[First[Part[IntegerDigits[Table[i^2, {i, 100}]], j]], {j, 100}]]

There are other elegant solutions of this problem, e.g.:

First /@ IntegerDigits@Table[i^2, {i, 100}] // ListLinePlot

But, the last code uses the function Map[] (/@) which is supposedly not known in Chapter 6 of the book.

I would use Table and Length like this:

list = IntegerDigits[Range[100]^2];
Table[Length[list[[i]]], {i, 1, Length[list]}]

I'm sure that there are other ways, but this one is pretty straightforward.

Hi Bill, thanks for your reply.

I think that I am expected to use functions that have been taught in the previous chapters ie. Table, Count, IntegerDigits, Length, Range. Map has not been taught yet.

Essentially, what I need to do is to Count the number of elements in each element of the list. I know that there are 100 elements in the list, each consisting of 1 or more elements.

So I need something like: Count[IntegerDigits[Table[n^2, {n, 100}]]] , which doesn't quite work. I strongly suspect the command is a combination of Count(or Length), IntegerDigits, Range, and perhaps Table.