There are a lot of approaches to solve Problem 6.10
Make a list line plot of the first digits of the first 100 squares.
But, we must use only the functions exposed in the first 6 chapters. So...
We can generate a list of the first 100 squares:
In[1]:= Table[i^2, {i, 100}]
Out[1]= {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, \
225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, \
841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, \
1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, 2601, \
2704, 2809, 2916, 3025, 3136, 3249, 3364, 3481, 3600, 3721, 3844, \
3969, 4096, 4225, 4356, 4489, 4624, 4761, 4900, 5041, 5184, 5329, \
5476, 5625, 5776, 5929, 6084, 6241, 6400, 6561, 6724, 6889, 7056, \
7225, 7396, 7569, 7744, 7921, 8100, 8281, 8464, 8649, 8836, 9025, \
9216, 9409, 9604, 9801, 10000}
In this list, we must find the digits of each number:
In[39]:= IntegerDigits@Table[i^2, {i, 100}]
Out[39]= {{1}, {4}, {9}, {1, 6}, {2, 5}, {3, 6}, {4, 9}, {6, 4}, {8,
1}, {1, 0, 0}, {1, 2, 1}, {1, 4, 4}, {1, 6, 9}, {1, 9, 6}, {2, 2,
5}, {2, 5, 6}, {2, 8, 9}, {3, 2, 4}, {3, 6, 1}, {4, 0, 0}, {4, 4,
1}, {4, 8, 4}, {5, 2, 9}, {5, 7, 6}, {6, 2, 5}, {6, 7, 6}, {7, 2,
9}, {7, 8, 4}, {8, 4, 1}, {9, 0, 0}, {9, 6, 1}, {1, 0, 2, 4}, {1, 0,
8, 9}, {1, 1, 5, 6}, {1, 2, 2, 5}, {1, 2, 9, 6}, {1, 3, 6, 9}, {1,
4, 4, 4}, {1, 5, 2, 1}, {1, 6, 0, 0}, {1, 6, 8, 1}, {1, 7, 6,
4}, {1, 8, 4, 9}, {1, 9, 3, 6}, {2, 0, 2, 5}, {2, 1, 1, 6}, {2, 2,
0, 9}, {2, 3, 0, 4}, {2, 4, 0, 1}, {2, 5, 0, 0}, {2, 6, 0, 1}, {2,
7, 0, 4}, {2, 8, 0, 9}, {2, 9, 1, 6}, {3, 0, 2, 5}, {3, 1, 3,
6}, {3, 2, 4, 9}, {3, 3, 6, 4}, {3, 4, 8, 1}, {3, 6, 0, 0}, {3, 7,
2, 1}, {3, 8, 4, 4}, {3, 9, 6, 9}, {4, 0, 9, 6}, {4, 2, 2, 5}, {4,
3, 5, 6}, {4, 4, 8, 9}, {4, 6, 2, 4}, {4, 7, 6, 1}, {4, 9, 0,
0}, {5, 0, 4, 1}, {5, 1, 8, 4}, {5, 3, 2, 9}, {5, 4, 7, 6}, {5, 6,
2, 5}, {5, 7, 7, 6}, {5, 9, 2, 9}, {6, 0, 8, 4}, {6, 2, 4, 1}, {6,
4, 0, 0}, {6, 5, 6, 1}, {6, 7, 2, 4}, {6, 8, 8, 9}, {7, 0, 5,
6}, {7, 2, 2, 5}, {7, 3, 9, 6}, {7, 5, 6, 9}, {7, 7, 4, 4}, {7, 9,
2, 1}, {8, 1, 0, 0}, {8, 2, 8, 1}, {8, 4, 6, 4}, {8, 6, 4, 9}, {8,
8, 3, 6}, {9, 0, 2, 5}, {9, 2, 1, 6}, {9, 4, 0, 9}, {9, 6, 0,
4}, {9, 8, 0, 1}, {1, 0, 0, 0, 0}}
We can generate a list of the first digits in each sub-list by different means. But, the beginner knows at this point only a few possibilities. First, we must identify every sub-list and its first element. For this, we use functions Part[] and First[]. Second, to generate a list, we use function Table[]:
In[43]:= Table[
First@Part[IntegerDigits@Table[i^2, {i, 100}], j], {j, 100}]
Out[43]= {1, 4, 9, 1, 2, 3, 4, 6, 8, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, \
4, 4, 5, 5, 6, 6, 7, 7, 8, 9, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, \
4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, \
8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 1}
And finally, we can use ListLinePlot[]:
ListLinePlot[
Table[First@Part[IntegerDigits@Table[i^2, {i, 100}], j], {j, 100}]]
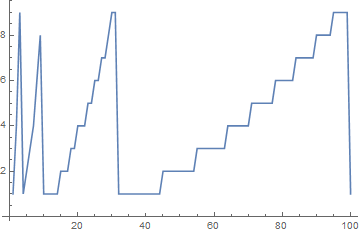
An equivalent code to the previous one:
ListLinePlot[
Table[First[Part[IntegerDigits[Table[i^2, {i, 100}]], j]], {j, 100}]]
There are other elegant solutions of this problem, e.g.:
First /@ IntegerDigits@Table[i^2, {i, 100}] // ListLinePlot

But, the last code uses the function Map[] (/@) which is supposedly not known in Chapter 6 of the book.